ノンパラメトリックベイズ(1)infinite GMM
元論文
[1]The Infinite Gaussian Mixture Model
http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.45.9111
論文中に"The likelihood for α may be derived from eq. (12)"とあるけど、何度読んでも、式(15)が式(12)から出るというのは無理がある気がするし、そもそも式(15)の1つ目の式は多分正確ではない。
おそらく、式(16)のChinese Restaurant Process(CRP)から出すのが正しい
具体的には
で、j番目のクラスに割り当てられた要素の数を$n_j$として、そのindexを昇順にI(1,j),...,I(n_j,j)とする。
と略記すると、クラスの数を$k$として
と積を並び替えられる。そして、CRPの定義(論文中の式(16))から
と計算できる。最終的に
という分布を得る。これは、Ewens分布と呼ばれるものになっている。
で、この分布に従って、n個の要素をk個のクラスに分割する確率は
となる。但し、S(n,k)は第一種Stirling数で、Γ(n+x)/Γ(x)をxのn次多項式と見た時のk次の係数に等しい。これが、式(15)の1つ目の式の正しい形と思う。第一種Stirling数の定義から、
が容易に分かる。nとkを固定してしまえば、式(15)の2つ目の式は、正しいので、論文通り、実装しても問題は生じない
逆に、Ewens分布からCRPを導出するのも、条件付き確率分布の定義通り計算すればいいので容易。
Ewens分布は、exchangeableなランダム分割のモデルの一つで、他の例として、Ewens分布の1パラメータ変形であるEwens-Pitaman分布は、Pitman-Yor過程とかで使われるらしい。exchangeableという性質は、上のEwens分布で、c_1,...,c_nの順番を任意に置換しても結合確率が変わらないことを指している。exchangebilityは、今はGibbsサンプリングが使えるために要求される性質と思っておけばいいっぽい。
cf)Exchangeable random variables
https://en.wikipedia.org/wiki/Exchangeable_random_variables
原理的には、exchangebleなランダム分割のモデルに対してinfinite GMMができるのだと思う(というわけで、Pitman-Yor mixture modelというものもあるらしい)。infinite GMMに於いて、Ewens分布を選ぶ理由は特になさそうに見えるけど
Exchangeable Gibbs partitions and Stirling triangles
https://arxiv.org/abs/math/0412494
によれば、Ewens-Pitman分布は、exchangeableなランダム分割としては、かなり一般的なモデルとなっているらしい
#論文[1]と同じようにして、Pitman-Yor mixture modelを実装してみようかと思ったけど、hyperparameterの更新式が複雑になった。これをどう乗り越えるべきか確信がなかった(力技で計算する以外の方法が思いつかなかった)ので、今回はpending
[余談]ちゃんと読んだわけではないけど、以下の論文2.4.2節によれば、Ewens分布は、Jack測度というものと同一視できるらしい(Jack測度は、自然数nの分割上で定められた測度)。論文で扱われている測度は、Macdonald測度とでも呼ぶべきだろうか(一般的に通りのいい名前は付いていないっぽい?)。Schur多項式->Jack多項式->Macdonald多項式という(1パラメータ、2パラメータ)変形に対応して、Plancherel測度->Jack測度->"Macdonald測度"という変形があるっぽい。
A probabilistic interpretation of the Macdonald polynomials
https://arxiv.org/abs/1007.4779
[余談2]arXiv:hep-th/0306238によれば"In many aspects, the set of partitions equipped with the Plancherel measure is the proper discretization of the Gaussian Unitary Ensemble (GUE) of random matrices"だそうである。Jack多項式のαは任意パラメータであるが、α=1,2,1/2の時は、ある対称空間上の球関数となる。一方、ランダム行列側では、ガウス型アンサンブルとして、GUE,GOE,GSEが知られている。α=1のJack測度がPlancherel測度で、その適当な極限は、GUEランダム行列の固有値の極限分布に一致するらしい(arXiv:math/9903176,arXiv:1402.4615)。というわけで、Ewens分布は数学的に見ても、非常に素性のよさそうな分布である
#ランダム行列について何も知らないけど、"hermitian random matrix ensembles"については、ある種の対称空間のCartan classとの対応があって、GUE/GOE/GSEは、その一例であるらしい(arXiv:cond-mat/0304363,arXiv:0707.0418)。今やランダム行列ユーザーの最大勢力は物理屋だと思うけど、これらのrandom matrix ensemblesは、class Bとclass DIII-oddを除けば、トポロジカル絶縁体・超伝導体の分類にも現れる(arXiv:0905.2029)。class Bとclass DIIIが物理で現れないというわけでもないっぽい(arXiv:cond-mat/0103089,arXiv:cond-mat/0103137)けど、ハミられている理由はよく分からない。最近は、"non-hermitian random matrices"も、応用があるそうな。
もうひとつ、論文[1]の式(17)の後半で、新しいクラスを割り当てる確率の計算で、積分が必要になるけど、
[2]Markov chain sampling methods for Dirichlet process mixture models
http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.115.3668
のAlgorithm8を使って積分を回避する。この論文には"However, the equilibirum distribution of the Markov chain defined by Algorithm 8 is exactly correct for any value of m"とあるのだけど、何故か分からない(mが大きければ、積分のモンテカルロ評価になるというのは論文に書いてある通りで明らかだけど)。このあとのステップで、同じ基底分布G0からφ_cをサンプリングすることになるので、そうなりそうな気もするけど...
全体の流れとしては、初期化が終わったら、以下の処理を繰り返す感じになる
(1)クラス割当の更新。論文[2]のalgorithm8を使う
(2)各クラスのcomponent parameters(今の場合、個々のクラスは、単一のガウス分布に対応しており、その平均と分散)をサンプリング。論文[1]の式(4)と(8)を使う
(3)hyperparametersの更新。論文[1]の適当な分布に従ってサンプリング。更新するhyperparameterは大きく分けると、基底分布G0のパラメータ(4つある)とDirichlet過程の集中度αの二種類となる
これを十分に繰り返せば、クラス割当/component parameters/hyperparametersの分布が得られるが、一番尤もらしい割当とパラメータが欲しいだけなので、それぞれの尤度を計算して一番いいものを選ぶ。十分多く繰り返せば、MAP推定値に近づくはず。
尤度は、DPGMMで対象データが生成される確率を計算する。ハイパーパラメータを決めれば、DPGMMに従うデータ点を生成していけるが、そのようにして実際に生成される点は、元の学習データとは、あまり似てないものになる公算が高そうな気がするけど、大丈夫なんだろうか。各クラスターの平均(と分散)は、基底分布G0に従って生成するので、特にクラスター数が少ない時には、元の学習データにあるクラスターとずれたところにクラスターを生成しても不思議ではなiい。そのへんは、通常の混合ガウス分布の方が、ずっと有能そうではある
#infinite GMMやDPGMMはノンパラメトリックベイズ的手法の一つと言うけど、ノンパラメトリックという言葉は全く正しくないように思うし、誤解と混乱を招く言い方の気がする。infinite GMMで使われているDPGMMのパラメータ(上でhyperparameterと書いてるもの)はαと基底分布のパラメータからなる。データの次元が一次元の場合は、基底分布のパラメータは4つ(正規分布の分が2つとガンマ分布の分が2つ)なので、合計5つのパラメータを与えれば、モデルを指定できる。一方、(一次元の)混合ガウス分布の場合は混合数をkとすると、平均と分散がk組、混合比がk-1個のパラメータで指定されるので、3k-1個のパラメータで定まる。一次元では、DPGMMは、混合数2の混合ガウス分布と同じ数のパラメータを持つ。
現在では、MCMC以外の、より高速な推定手法も提案されてはいるようだけど、特に調べてはいない。
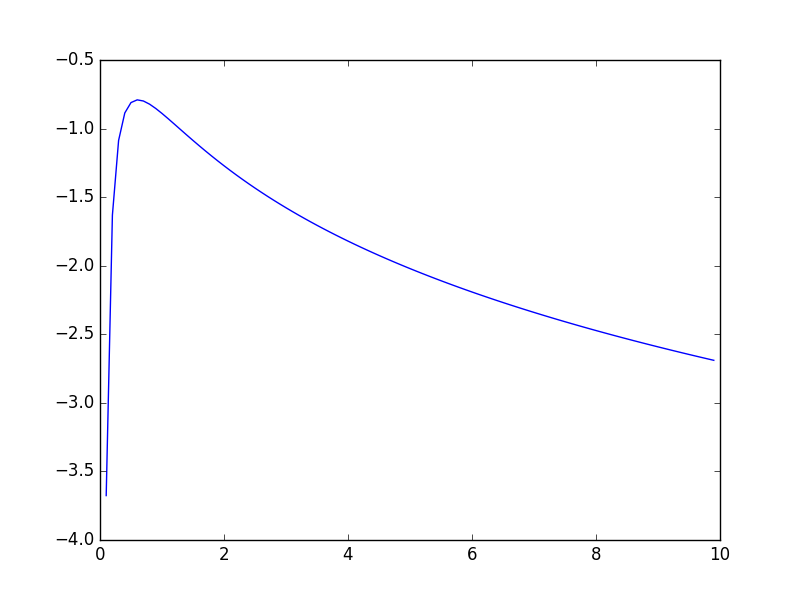
問題として、βの分布が、k=1の時、log-concaveではない気がする(ので、ARSが失敗する場合がある)。以下のコードで、対数確率密度関数のplotをしてみたけど、k=1の時は、xが2か3あたりを超えると、微妙に凹でない
import matplotlib.pyplot as plt from scipy.special import gammaln s,w=np.array([ 0.69756949 ]) , 1.159287098021641 k = len(s) x = np.arange(1 , 100)*0.1 y = -k*gammaln(x/2) - 1/(2*x) +((k*x-3)/2)*np.log(x/2) + (x/2)*np.sum(np.log(s*w)) - (x*w/2)*np.sum(s) plt.plot(x, y) plt.show()
αも同様に、log-concaveでないと思う(プロットして見ても、かなり分かりにくいが、kが小さい時の方が、"凹度"は高い気がする)
import matplotlib.pyplot as plt from scipy.special import gammaln k,n=1,500 x = np.arange(1,101)*0.5 y = (k-3/2)*np.log(x) - 1/(2*x) + gammaln(x) - gammaln(n+x) plt.plot(x, y) plt.show()
(私が間違ってるのでないとすると)結構イイカゲンな論文だな、という印象なんだけど、どうなんだろう
以下に実装したコードを置いておく。面倒なので、データが一次元空間上に分布している場合のみを考えている。αとβのサンプリングは、論文に従ってARSで行っているものの、上で書いた理由で、正しくはない(し、エラーを起こす場合がある)。今回の目的はサンプリングではなく、MAP推定なので、αとβのサンプリングが多少悪くても、よかろうと思って、そのままにしてある
実際に、DPGMMでデータを生成して、infinite GMMでfittingして見ると、データが一次元のせいもあって、クラス間の分離が悪い場合は、本来存在するより少ないクラスしか出てこない場合があるように思える。対数尤度を計算してみると、infinite GMMで計算した方が高くなっているので、実装が間違ってるわけでもないと思う
まぁ、さしあたって、infinite GMMは、ノンパラメトリックベイズの一番簡単な例題として勉強しただけで、本来の目的ではないので、とりあえず、諸々の問題点・課題(α、βのサンプリング、高次元データ対応etc.)は、そのままにしておいて、次に進む
"""
This is an implementation of the following paper written in python 3.5
(The only univariate case is supported)
The Infinite Gaussian Mixture Model
http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.45.9111
"""
import numpy as np
import math
from scipy.special import digamma
def rnd_from_piecewise_exponential(coeffs , intercepts , points):
"""
density function h(x) in [points[i] , points[i+1]]
h(x) = exp(coeffs[i]*x + intercepts[i])
"""
assert(len(coeffs)==len(intercepts)),(coeffs,intercepts)
assert(len(coeffs)+1==len(points)),(coeffs,points)
u = np.random.random()
CDF = [0.0] #--cumulative density value at each points
for i in range(len(points)-1):
z_cur = points[i]
z_next = points[i+1]
assert(z_cur<z_next),(points)
a = coeffs[i]
b = intercepts[i]
if a!=0.0:
r = np.exp(b)*(np.exp(a*z_next) - np.exp(a*z_cur))/a
else:
r = (znext-z)*np.exp(b)
assert(not np.isinf(r)) , (coeffs , intercepts , points)
r0 = CDF[-1]
CDF.append( r + r0 )
u = CDF[-1]*u #--CDFが正規化されてないので
for i in range(len(points)-1):
if CDF[i] < u and u <=CDF[i+1]:
a = coeffs[i]
b = intercepts[i]
z = points[i]
"""
compute t such that
( exp(a*t+b) - exp(a*z+b) )/a == u - CDF[i]
"""
if a!=0.0:
t0 = a*(u - CDF[i]) + np.exp(a*z+b)
assert(t0 > 0.0),t0
t = ( np.log(t0) - b )/a
else:
t = (u - CDF[i])/np.exp(b) + z
assert(t >= z and t <= points[i+1]),(t,z,points[i+1])
return t
assert(False),("rnd_from_piecewise_exponential",u,CDF,points,coeffs,intercepts)
def ars(h , hprime , points , support=(0 , np.inf)):
xs = [x for x in points]
xs.sort()
assert(len(xs)>0)
assert(xs[-1]>0)
while hprime(xs[-1])>=0.0:
xs.append( 2*xs[-1] )
while 1:
xs.sort()
x0 = xs[0]
xN = xs[-1]
zs = [support[0]]
coeffs = []
intercepts = []
for i in range(len(xs)-1):
x = xs[i]
xnext = xs[i+1]
assert(xnext>x)
zi = (h(xnext) - h(x) - xnext*hprime(xnext)+x*hprime(x))/(hprime(x) - hprime(xnext))
assert(zi>zs[-1]) , (zi,zs,xs , xnext,h(x) , h(xnext) , hprime(x) , hprime(xnext))
zs.append( zi )
coeffs.append( hprime(x) )
intercepts.append( h(x) - hprime(x)*x )
zs.append( support[1] )
coeffs.append( hprime(xN) )
intercepts.append( h(xN) - hprime(xN)*xN )
y = rnd_from_piecewise_exponential(coeffs , intercepts , zs)
w = np.random.random()
ukval = 0.0
assert(not np.isinf(y)),(coeffs,intercepts,zs,y)
for i in range(len(zs)-1):
if zs[i]<=y and y<=zs[i+1]:
ukval = h(xs[i]) + (y-xs[i])*hprime(xs[i])
break
if w<=np.exp(h(y) - ukval):
return y
else:
xs.append( y )
def gen_alpha(k , n):
def pdfln(x):
C = sum([np.log(i) for i in range(1,n+1)])
return C + (k-3/2)*np.log(x) - 1.0/(2*x) + math.lgamma(x) - math.lgamma(n+x)
def pdfln_prime(x):
return (k-3/2)/x + 1.0/(2*x*x) + digamma(x) - digamma(n+x)
while 1:
try:
return ars(pdfln , pdfln_prime , [0.1 , 1.0 , 3.0])
except:
continue
def gen_beta(s , w):
def pdfln(x):
k = len(s)
return -3*math.log(x)/2 - 1.0/(2*x) - k*math.lgamma(x/2)+(k*x/2)*math.log(x*w/2) + np.sum((x/2-1)*np.log(s) - (x*w/2)*s)
def pdfln_prime(x):
k = len(s)
return -(k/2)*digamma(x/2) + 1.0/(2*x*x) + (k/2)*math.log(x/2) + (k*x-3)/(2*x) + np.sum(np.log(s) - w*s)/2 + k*math.log(w)/2
while 1:
try:
return ars(pdfln , pdfln_prime , [0.1 , 1.0 , 3.0])
except:
continue
def rnd_gamma(alpha,theta):
return np.random.gamma(alpha/2 , 2*theta/alpha)
def pdf_normal(x , mean , precision):
return math.sqrt(precision/(2*np.pi))*np.exp(-precision*(x-mean)**2/2)
def pdf_gamma(x , alpha,theta):
lprob = (alpha/2-1)*np.log(x) - alpha*x/(2*theta) - math.lgamma(alpha/2) - (alpha/2)*(math.log(2*theta/alpha))
return math.exp(lprob)
#-- normal gamma distribution pdf
#-- for multivariate case, this should be normal wishart distribution pdf
def pdf_G0(mu , s , lam , r , beta , w):
return pdf_normal(mu ,lam , r)*pdf_gamma(s,beta,1.0/w)
def pdf_lewens(k,n,alpha,ns):
return (k*np.log(alpha)) + sum([math.lgamma(n) for n in ns]) - (math.lgamma(n+alpha) - math.lgamma(alpha))
class DPGMM:
def __init__(self , alpha , lam , r , beta, w):
self.alpha = alpha
self.lam = lam
self.r = r
self.beta = beta
self.w = w
self.cnts = []
self.params = [] #-- component parameters
self.indicators = [] #-- for debug
def __iter__(self):
return self
def __next__(self):
N = sum(self.cnts)
k = len(self.cnts)
probs = [n/(N+self.alpha) for n in self.cnts]
probs.append( (self.alpha)/(N+self.alpha) )
c = np.random.choice( list(range(k+1)) , p=probs)
self.indicators.append(c)
if c<k:
mu,s = self.params[c]
self.cnts[c] += 1
else:
mu = np.random.normal(self.lam , math.sqrt(1.0/self.r))
s = rnd_gamma(self.beta , 1.0/self.w)
self.params.append( (mu,s) )
self.cnts.append( 1 )
return np.random.normal(mu , math.sqrt(1.0/s) )
def likelihood(self,xs):
k_rep = len(self.cnts)
N = len(self.indicators)
Ptmp = pdf_lewens(k_rep,N, self.alpha, np.array(self.cnts))
for j,(m,s) in enumerate(self.params):
mask = (np.array(self.indicators)==j).astype(int)
Ptmp += np.sum( mask*np.log(pdf_normal(xs,m,s)) )
Ptmp += np.log( pdf_G0(m,s,self.lam , self.r, self.beta, self.w) )
return Ptmp
def iGMM(xs , iter=200):
assert(type(xs)==np.ndarray)
N = len(xs)
mean_all = np.sum(xs)/N
var_all = np.sum(xs**2)/N - mean_all*mean_all
stdev_all = math.sqrt(var_all)
best_indicators = np.zeros(len(xs) , dtype=np.int)
best_alpha = 1.0/rnd_gamma(1.0 , 1.0)
best_beta = 1.0/rnd_gamma(1.0 , 1.0)
best_lambda = np.random.normal(mean_all , stdev_all)
best_r = rnd_gamma(1 , 1.0/var_all)
best_w = rnd_gamma(1 , var_all)
best_mparams = [mean_all]
best_sparams = [1.0/var_all]
k_rep = 1
Ptmp = 0.0
for j,(m,s) in enumerate(zip(best_mparams,best_sparams)):
mask = (best_indicators==j).astype(int)
Ptmp += np.sum( mask*np.log(pdf_normal(xs,m,s)) )
Ptmp += np.log( pdf_G0(m,s,best_lambda,best_r,best_beta,best_w) )
Pmax = Ptmp
#print(Pmax)
for it in range(iter):
#-- step(1) update class indicators
h = N
k_rep = np.max( best_indicators ) + 1
assert(h >k_rep)
new_indicators = np.copy( best_indicators )
top_mparams = np.zeros(h)
top_sparams = np.zeros(h)
top_mparams[:k_rep] = np.copy(best_mparams)
top_sparams[:k_rep] = np.copy(best_sparams)
top_mparams[k_rep:] = [np.random.normal(best_lambda , math.sqrt(1.0/best_r)) for _ in range(0,h-k_rep)]
top_sparams[k_rep:] = [rnd_gamma(best_beta , 1.0/best_w) for _ in range(0,h-k_rep)]
for (n,x) in enumerate(xs):
top_nums = np.bincount( new_indicators )
k_rep = len(top_nums)
c = new_indicators[n]
top_nums[c] -= 1
Fvals = np.array([pdf_normal(x , mu , s) for (mu,s) in zip(top_mparams,top_sparams)][:h])
if top_nums[c]==0:
k_rep -= 1
weights = np.ones(h)*(best_alpha/(h-k_rep))
weights[:k_rep+1] = top_nums
weights[c] = (best_alpha/(h-k_rep))
else:
weights = np.ones(h)*(best_alpha/(h-k_rep))
weights[:k_rep] = top_nums
Fvals *= weights
Ftot = np.sum(Fvals)
new_c = np.random.choice(list(range(h)) , p=Fvals/Ftot)
if top_nums[c]==0:
if (new_c==c or new_c>=k_rep):
new_indicators[n] = c
else:
new_indicators[n] = new_c
mask = (new_indicators>=c).astype(int)
new_indicators -= mask
top_mparams[c:h-1] = top_mparams[c+1:h]
top_sparams[c:h-1] = top_sparams[c+1:h]
top_mparams[h-1] = 0.0
top_sparams[h-1] = 0.0
h -= 1
elif new_c>=k_rep:
#-- swap new_c and k_rep
new_indicators[n] = k_rep
top_mparams[k_rep],top_mparams[new_c] = top_mparams[new_c] , top_mparams[k_rep]
top_sparams[k_rep],top_sparams[new_c] = top_sparams[new_c] , top_sparams[k_rep]
else:
new_indicators[n] = new_c
#-- step(2) update component parameters
k_rep = np.max( new_indicators ) + 1
new_mparams = []
new_sparams = []
for j in range(k_rep):
mask = (new_indicators==j).astype(int)
nj = np.sum(mask)
ybar_j = np.sum(mask*xs)/nj
sj = top_sparams[j]
mu_j = np.random.normal((ybar_j*nj*sj*best_lambda*best_r)/(nj*sj+best_r) , math.sqrt(1.0/(nj*sj+best_r)))
var_j = np.sum( mask*(xs-np.ones(N)*mu_j)**2 )
sj = rnd_gamma(best_beta+nj , (best_beta+nj)/(best_w*best_beta+var_j))
new_mparams.append( mu_j )
new_sparams.append( sj )
#-- step(3) update hyperparameters
new_lambda = np.random.normal( (mean_all/var_all+best_r*sum(new_mparams))/(1.0/var_all+k_rep*best_r) ,
math.sqrt(1.0/(var_all+k_rep*best_r)) )
new_r = rnd_gamma(k_rep+1 , (k_rep+1)/(var_all + sum([(x-new_lambda)**2 for x in new_mparams])))
new_w = rnd_gamma(k_rep*best_beta+1 , (k_rep*best_beta)/(1.0/var_all + best_beta*sum(new_sparams)))
new_beta = gen_beta(np.array(new_sparams) , new_w)
new_alpha = gen_alpha(k_rep , N)
#-- compute P
Ptmp = pdf_lewens(k_rep,N,new_alpha,np.bincount(new_indicators))
for j,(m,s) in enumerate(zip(new_mparams,new_sparams)):
mask = (new_indicators==j).astype(int)
Ptmp += np.sum( mask*np.log(pdf_normal(xs,m,s)) )
Ptmp += np.log( pdf_G0(m,s,new_lambda,new_r,new_beta,new_w) )
P = Ptmp
#print(P , k_rep)
if P>Pmax:
best_indicators = new_indicators
best_mparams = new_mparams
best_sparams = new_sparams
best_alpha = new_alpha
best_beta = new_beta
best_r = new_r
best_w = new_w
best_lambda = new_lambda
Pmax = P
else:
pass
return (best_indicators , best_mparams , best_sparams , best_alpha,Pmax)
#-- simple test
if __name__=="__main__":
m = DPGMM(1.1,0.0 , 15.0 , 1.1,0.5)
dat=[]
for _ in range(200):
dat.append(next(m))
dat=np.array(dat)
print( iGMM(dat) )
今後の目標としては、
・infinite HMMを理解する。階層Dirichlet過程というものを使うらしい
・infinite PCFGを理解する
The Infinite PCFG using Hierarchical Dirichlet Processes
https://cs.stanford.edu/~pliang/papers/hdppcfg-emnlp2007.pdf
あたり。Dirichlet過程を使っているものは、須く、Pitman-Yor過程に一般化できるのだと思うので、必要に応じて理解したい。
やりたいこととしては、CCG(Combinatory Categorial Grammar)の確率版であるPCCGを作れるので、"infinite PCCG"ができないだろうかというあたり。CCGはCFGより強いが、どっちもCYK parsingでparseできるし、infinite PCFGができるなら、infinite PCCGができない道理はなさそうな気がする。まぁ、未知の言語の文法構造を、人出によるタグ付けとかなしで、推定できるようになれば嬉しいのだけど、infinite PCFGが流行ってるようにも見えないので、どうなのか(そもそも、文法推論業界で得られてる知見によれば、正規表現程度でも、"ちゃんと"学習するには、正例のみだけではダメで、負例が必要ということなので、もっと強いCFGやCCGでは、尚更、負例の提示が必要そうだけど、今のinfinite PCFGとかは多分正例しか食べ(れ)ないので、そのへんどうなっているか理解したい)