表現論と信号処理
SU(1,1)あるいは、SL(2,R)の既約ユニタリ表現には、limit of discrete seriesと呼ばれるクラスのものが、2つある(一方は、他方の反傾表現になっている)。limit of discrete seriesは、直訳すると、"離散系列の極限"だけど、極限離散系列とかいう言葉は、耳慣れない気がするので、そのまま、limit of discrete seriesと書くことにする(検索すると、極限離散系列表現でも、何件か引っかかる)。
1947年に、Bargmannが、SL(2,R)の既約ユニタリ表現を分類した時、とある可約な連続主系列表現を直和分解することで、2つのlimit discrete seriesを構成したらしい。一旦、構成されてしまうと、特に複雑なものでもないので、何気なく、見過ごしてしまいそうだけど、Bargmannの構成は、古典的なPaley-Wienerの定理を、表現論的に捉えたものだとも解釈できる(多分、Bargmannは、別に、そんな風には理解してなかったんじゃないかと思うけど)。
Paley-Wienerの定理は、Hardy spaceのFourier変換による像が、[0,∞)上のL^2関数に等しいと書かれることもあるけど、L^2(R)を、(-∞,0]上のL^2関数と[0,∞)上のL^2関数の空間に直和分解できると見ることもできる。この2つの直和成分上に、2つのlimit of discrete seriesを実現できる。
実信号をFourier変換して、正の周波数成分のみを逆Fourier変換したものを、解析信号と呼ぶ(Gabor,1946)。これは、L^2(0,∞)を逆Fourier変換で戻しているので、解析信号は、Hardy spaceの元になる。当然、負の周波数成分のみを逆Fourier変換することも可能で、実数上の二乗可積分関数空間が、解析信号のなすHardy spaceと"反解析信号"のなす空間と、2つの空間に直和分解する。
また、実信号に対して、この信号を実部とする解析信号の虚部を与える変換は、ヒルベルト変換と呼ばれている。Hilbertは、Riemann-Hilbert問題の特殊ケースを解くために、この変換を導入したと、Wikipediaに書いてある。ヒルベルト変換は、物理では、Kramers-Kronigの関係式で現れる。
これらの定理や概念が発表された時期をまとめると、以下のようになる。
1926~27 Kramers-Kronigの関係式
1934 Paley-Wiener theorem
1946 解析信号(Gabor)
1947 SL(2,R)の既約ユニタリ表現の分類,特にlimit of discrete seriesの構成(Bargmann)
似たようなことが、異なる文脈で、何度も発見されて重要視されているので、多分、重要なんだろう
[0,∞)上のL^2関数空間は、Laguerre関数(Laguerre多項式に、exp(-x/2)をかけた関数)を、正規直交基底に持つことは、よく知られた事実である。Laguerre関数のFourier変換は、Wiener rational functionと呼ばれることがある。これを、更に、"Cayley変換"して、S^1上の関数と見ると、"exp(i n θ)"(nは非負整数)が得られる。指数関数/Wiener rational function/Laguerre functionという3種類の基底に対して、それぞれ、limit of discrete seriesの実現を与えることが出来る。円周上の関数としては、n<0に対しても、exp(i n θ)を考えたほうが自然であるけど、この部分に、丁度、もうひとつのlimit of discrete seriesを実現できる。そして、(-∞,0]上のL^2関数から、同様の操作を経ることで、得ることもできる
もう少し詳しい式は、以下に書いた
su(1,1)のlimit of discrete series
https://vertexoperator.github.io/2019/02/15/limit_of_discrete_series.html
su(1,1)のlimit of discrete seriesは、最高あるいは最低ウェイト表現で、この点については、su(1,1)のdiscrete seriesでも同様であるけども、二乗可積分表現でないため、連続ウェーブレット変換を定義することはできない(admissible vectorを持たない)。SL(2,R)の群作用は簡単に書けるけど、それが重要な理由は、よく分からない
ヒルベルト変換の工学的な応用としては、包絡線を書くのに使われる。物理や工学系のテキストで、殆ど周期的に時間変動する量を、瞬時値の一周期(あるいは適当な長さ)の時間平均として定義する、みたいなことが、よくある。この定義は、現実に観測される信号は、完全に周期的でないので、実用上は困る。ヒルベルト変換して、得られた解析信号の絶対値を定義とすれば、計算できる量となる。
偏角は位相を与えるわけだけど、例えば、音声信号(有声音)のピッチマーキング(周期点を発見すること)は、難しい問題で、完全な方法というのは、今も存在しない。ということで、音声信号にヒルベルト変換を施して、位相情報を取ると、どうなるか見てみた。
音声データは、
日本声優統計学会
http://voice-statistics.github.io/
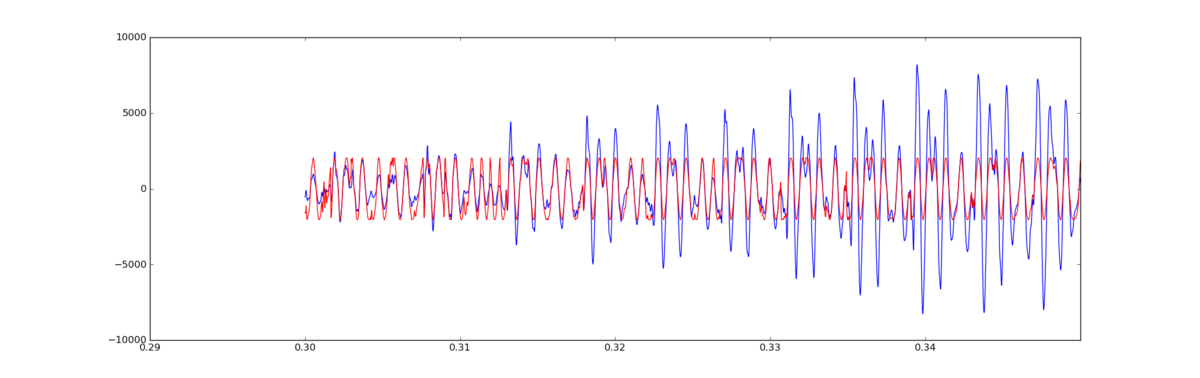
のtsuchiya_normal_100.wavを使用。冒頭の0.3〜0.35秒の区間("アーリー"の"あ"の音の一部)を抽出して、ヒルベルト変換を施し(scipyに含まれている)て、偏角を得、偏角のcosineを(見やすいように)定数倍して、音声信号と重ねた
青いのが、元音声の振幅で、赤いのが、ヒルベルト変換して得た位相(のcosine取って定数倍したもの)。まぁ、ピッチマーキングに使うことはできなそうだけど、ピークピッキングには使えそうな感じかもしれない
一般に、
の形の関数は、so(3,2)の極小表現のある実現(massless Klein-Gordon方程式の正エネルギー解を運動量空間で書いた時の基底)でも出てくる
so(3,2)の極小表現と波動方程式(書きかけ)
https://vertexoperator.github.io/2019/03/17/AdS4.html
多分、負エネルギー解の方も、同じような形の基底で書けるのだろう。数学的には、上の話の一般化というわけでもないのだけど、物理的には、関係が深そうな話ではある