自由流線理論による揚力計算

何となしに目にした1951年の古い論文に、面白い計算が書かれていた。

死水域を伴う任意翼型の特性
https://doi.org/10.2322/jjsass1948.4.30

一様流中に(任意の迎角を持って)置かれた平板翼で、後端と上面の途中に剥離点がある場合、揚力がどうなるか計算している。非粘性流体力学のバリエーションなので、剥離位置自体は、理論的に決めるわけではなく、外部パラメータとして与えられる。特に、自由流線理論に基づく計算に於いて、剥離点が限りなく後端に近い極限を取れば、後流が無限に薄い流れをモデル化できそうな気がする(これは、正しくないけど)

論文の計算方法は、今井功『流体力学(前編)』(裳華房)の7章"不連続流"に説明されているのと同じ。この本も、初版は1973年とあるので、古い本ではある。不連続流の理論や、死水理論と呼ばれることもあるけど、自由流線理論(free streamline theory)という名前も使われるようなので、ここでは、この名前を使う(自由流線は、圧力が流線に沿って一定であることを指す;今井功『流体力学(前編)』§51)

迎角を大きくしていく時、後端から前端へ剥離点が移動するパターンが見られるのは、後縁失速を起こす場合で、NACA4421翼型などで見られるらしい。自由流線理論によるモデル化が一番適切っぽいのは、このケースかもしれない。

平板翼では、前端で剥離した流れが、上面途中で再付着する剥離泡の形成が、迎角がかなり小さい時でも起きるらしいけど、自由流線理論で計算される流れでは、剥離泡は出ない(標準的な揚力計算でも出ないけど)(今井功『流体力学(前編)』§34,Q3参照)。平板翼などで迎角を大きくしていくと、再付着点が後端に移動していき、やがて、前端で剥離した流れが再付着しなくなって揚力を失うらしい(薄翼失速と呼ばれる)

上論文中で扱われているNACA4412は、前縁失速と呼ばれるパターンを示し、迎角15度くらいで、突然、前縁で剥離するようになって揚力を失うっぽい。多分、現代のCFDなら、迎角と翼型(とレイノルズ数)を決めた時、剥離パターンや剥離位置(や再付着がある場合は再付着点)を決めることはできるかもしれないけど、解析的に計算できるケースは、ほぼないと思われる。

歴史的には、標準的な揚力計算の方は、平板翼や円弧翼だけでなく、実際の翼型で数値計算して、揚力係数のみでなく、翼面上の圧力分布を、定量的に、かなり再現することが確認されている。とはいえ、自由流線理論による計算でも、実際の翼型に対して、定量的によい結果を与える可能性は否定できない。

【翼型】翼型のデータは、検索すると拾って来れる。以下は、いくつか描画してみたもの。少なくとも、私には、これを見ても何もわからないが
f:id:m-a-o:20190921152626p:plain:w300f:id:m-a-o:20190921152637p:plain:w300f:id:m-a-o:20190921152646p:plain:w300

【補足:揚力の数値計算(CFD以前)】平板翼や円弧翼、Joukowski翼型などで揚力が解析的に決定された後、1920年代に、薄翼理論(thin airfoil theory,今井功『流体力学(前編)』§49の内容)が作られた。真に任意翼型で適用できる計算法は、1930年代に開発された(今では、教科書で見ることもない。1960年代に現れたパネル法は、航空工学の教科書で説明されているのを見かける)。最初のものは、アメリカのTheodore Theodorsenが考案した方法で、1931年に、NACA technical report 411として、出版された。ここで、Clark Y翼型に対して、実験値との比較も行われている。また、NACA technical report 452では、NACA M6翼型に対して、同様の比較が行われている
[NACA-TR-411] Theory of wing sections of arbitrary shape
https://ntrs.nasa.gov/search.jsp?R=19930091485

[NACA-TR-452] General Potential Theory of Arbitrary Wing Section
https://ntrs.nasa.gov/search.jsp?R=19930091527

1933年に、Theodorsenの方法を、実際の翼型20個と、いくつかの異なる迎角に対して適用して、圧力分布を計算した報告が出ている。
[NACA-TR-465] Determination of the theoretical pressure distribution for twenty airfoils
https://ntrs.nasa.gov/search.jsp?R=19930091540

任意形状翼型に適用できる別の方法として、1938年には、守屋富次郎という人が、別の方法を提案している。こっちは、Fourier級数の形で与えた翼型形状に対して、速度ポテンシャルの形をFourier係数を使って具体的に書き、循環を計算している。このような手法は、層流翼の開発で役立ったらしい
任意の翼型の特性を求める一つの方法
https://doi.org/10.14822/jjsass1934.5.33_7


【補足:"Kuttaの条件"の呼称】Kuttaの条件は、後端に於ける流速が有限になる(後縁角が正の場合は0になる)という境界条件の一種で、今井功『流体力学(前編)』§33では、"Kuttaの条件あるいはJoukowskiの仮定"と書かれている。ランダウ・リフシッツの教科書では、Zhukovskii-Chaplyginの条件と呼ばれている。誰が何を考えたのか、原論文を参照できなかったけど、以下の論説に、事情が書かれている。

クッタとジュコフスキーの翼理論
https://www.jstage.jst.go.jp/article/nagare1970/5/4/5_4_1/_article/-char/ja/

まず、1902年に、Kuttaが(迎角0度の)円弧翼に働く揚力を決定した(リリエンタールの測定結果に影響を受けたと言われるが、リリエンタールの測定とは有限翼幅補正を入れても定量的には合わないので、この不一致をどう考えたのかは分からない。とにかく、迎角0度でも揚力が働き、流速の二乗に比例するという結果は得られた)。従って、Kuttaは"Kuttaの条件"そのものか、それと同値な仮定をしたのだろう。この仕事は、特に知られることもなく、1906年に、Joukowskiが、いわゆるKutta-Joukowskiの定理を一般的な状況下で示した。けれど、Joukowskiは、循環の値を決める方法は、与えなかったようである。上論説中には『これに対して後縁の条件は,Kuttaひとりに帰すべきものである。少なくとも1910年以前のZhukovskiの論文には,この条件に言及したものがないのである。したがって,"Kuttaの条件"と呼ぶのが妥当であって,Zhukovskiの名を加える必要はない』と書いている。

少し後の方には、『ここで付け加えておきたいのは,同じ1910年に発表されたロシアのChaplyginの論文である。ChaplyginはKuttaの発表(1910)を知らないで,まず迎角のある円弧翼の揚力を計算し,さらに二つの円弧から成る三日月翼断面その他の場合を取扱っている』ともあり、Chaplyginは、循環の値を決定しているようなので、Kuttaの条件に相当する条件を置いたのだろう。なので、Kutta-Chaplyginの条件と呼ぶのが妥当かもしれない。そう呼ぶ人もいないわけではないっぽい。

Chaplyginの1910年の論文というのは、以下で読めるっぽいけど、(ロシア語が)読めない
О давлении плоскопараллельного потока на преграждающие тела (к теории аэроплана)
On the pressure of plane-parallel flow on the blocking bodies (to the theory of an airplane)
http://gpntb.dlibrary.org/ru/nodes/5240-chaplygin-s-a-o-davlenii-ploskoparallelnogo-potoka-na-pregrazhdayuschie-tela-k-teorii-aeroplana-m-1910

20世紀初頭の物理学者にとっては、複素解析や等角写像の理論は、まだ標準的なレパートリーになってなかったかもしれない。リーマンの写像定理が1851年で、Christoffelが、Schwartz-Christoffel変換の論文を書いたのが1867年らしい。流体力学自体は古い分野だけど、必要な数学ができて、計算できるようになったという側面もあったのだろう



自由流線理論の歴史については、

Ideal free streamline flow over a curved obstacle
https://www.sciencedirect.com/science/article/pii/0377042795002723

のIntroductionに、少し書かれているけど、適当に補うと、以下のような感じ。

流れの中に物体があるばあい、物体が流体から受ける力を計算するには、物体の表面に働く圧力を求め積分すればいい(今井功『流体力学(前編)』§30参照。翼に働く表面摩擦の場合は、せん断応力を積分しないといけないけど)。このことは、18世紀には既に分かっていて、この方針で計算した結果、ダランベールのパラドックスが導かれた(今井功『流体力学(前編)』§28参照)。

実験的には、(水中でも空気中でも)抗力が流速の二乗に比例するという結果は何度も確認されたし、ダランベール自身も、水中で平板に働く抗力を測定している。ダランベールが理論的に考えたような流れが生じるのは、レイノルズ数が低い時のみ(今井功『流体力学(前編)』§2、1-1図)で、一方、実測したような条件下では、後流ができ、抗力の主要な部分は圧力抵抗に由来する(低レイノルズ数で正しいStokes抵抗則は1851年に発表されている)

自由流線理論の開拓者は、Helmholtz(1868)らしい。今井功『流体力学(前編)』§52に、噴流への適用が書かれていて、このへんの仕事っぽい(?)。"free streamline"という名前は、Kirchhoffによるとされる。


1876年に、Lord Rayleighは、平板の後流部を死水域と仮定して、一様流に対して(大きな)迎角を持つ平板に働く抗力を計算した。但し、剥離は、平板の前端と後端で起こると仮定している(この流れは、Helmholtz流と呼ばれることがある)。この結果は、今井功『流体力学(前編)』§53に説明されている。論文は、以下にある

On the resistance of fluids
https://www.tandfonline.com/doi/abs/10.1080/14786447608639132?journalCode=tphm16

抗力の計算値は、測定値の半分弱でしかなかったけど、(1+4/π)倍すると、1798年のVinceの測定結果(水中の測定らしい)とよく一致すると書いてある。この謎の定数倍因子について、論文では"The fourth column represents the law of resistance according to the formula now proposed, a factor being introduced so as to make the maximum value unity"と書かれている。補正がなければ、流れに対して垂直に立てた平板の抗力係数は、C_D = 2\pi/(4 + \pi) \approx 0.88で、補正因子を掛けると、C_D=2.0を得る。こうして、(ニュートン流近似は別として)非粘性流体力学の範囲で、初めて、抗力が流速の二乗に比例するという結果が得られた

補正因子が必要になるのは、死水域の圧力を、静圧に等しいとしたためで、実際は負圧になっているとされる。適当な背圧を外部パラメータとして与えてやれば、正しい結果になるというのが、論文で与えられた謎の補正因子の現代的解釈だと思う。今井功『流体力学(前編)』$55では、背圧を無次元の形で表した空洞係数(cavitation number)を導入して(Q=0は、背圧が静圧と等しい場合で、上記の論文の補正は、Q=4/πに相当する)、"C_D(Q)=C_D(0)(1+Q)によって、物体の受ける抗力を近似できると考えられるが、一般的な証明は、いまのところ与えられていない"と書かれている。

こうして、外部パラメータが必要ではあるけど、一様流中の平板に働く(迎角が大きい時の)圧力抵抗が計算できるようになった。同じ方法で、揚力も計算できるけど、論文には何も書かれていない。前縁で剥離が起こるようになって以後、大迎角に対する揚力係数の実験値を、見かけることが、あまりない気がするのだけど、

Aerodynamic characteristics of seven symmetrical airfoil sections through 180-degree angle of attack for use in aerodynamic analysis of vertical axis wind turbines
https://doi.org/10.2172/6548367

に、いくつかの対称翼に対して、迎角、レイノルズ数ごとのデータが記載されている。迎角と揚力係数の関係を、この論文の実験データの一つと、Helmholtz流(空洞係数の補正あり)に対するC_L=(1+4/\pi)\dfrac{2\pi\sin(\alpha)\cos(\alpha)}{4+\pi\sin(\alpha)}、Kutta-Jouwkoski流に対するC_L = 2\pi \sin(\alpha)(今井功『流体力学(前編)』式(33.15))を、プロットしてみる。対称翼なので、負の迎角は、見る必要がない。

f:id:m-a-o:20190824140049p:plain
迎角と揚力係数

元々のダランベールのパラドックスは、円柱に対する計算だったけど、Rayleighは、円柱に自由流線理論を適用した計算もしてない。代わりに(?)、1879年の論文で、Magnus効果(1852年、ドイツのHeinrich Magnusが報告していた)について考察し、揚力の計算を試みている。論文では、円柱に対するKutta-Joukowskiの定理が書かれているけど、循環の具体的な値は決めてない(ので定量的な予測はされてない)。

On the Irregular Flight of a Tennis-Ball
https://doi.org/10.1017/CBO9780511703966.054

この説明は、今でもよく見かけるけど、飛翔するテニスボールを、このようにモデル化するのは(多分)正しくない。飛翔するテニスボールの場合、レイノルズ数は、10^5オーダー(空気の動粘性係数の逆数くらい)で、ボール自身が回転するので、厄介であるけど、無回転の時と同様、背後に、後流が発生しているらしい。この後流領域を、死水領域としてモデル化することが妥当かは知らないけど、どっちにしろ、何も断らずにKutta-Joukowskiの定理を適用していい問題ではないと思う

cf)マグヌス効果の物理的メカニズムについて
https://www.jstage.jst.go.jp/article/jjsass/57/667/57_667_309/_article/-char/ja

【Magnus効果の応用】1920年代に、ドイツのAnton Flettnerという人が、風を受ける回転円筒を備え、Magnus効果で推進するローター船を作ったとされている。回転する円筒で飛行する航空機(Rotor airplane/Flettner airplane)も、試作されたことはあるようだけど、あまり記録がない。Flettnerは、その後、初期のヘリコプター開発にも関わったようだけど、Flettnerが、Flettner airplaneを作ったということは、ないっぽい。ローター船の場合、風速は、数m/sだろうけど、直径は約4メートルだったらしいので、レイノルズ数は、テニスボールの場合と同程度か、それより大きいと考えられるので、単純にKutta-Joukowskiの定理で、推力を説明するのは、正しくない結果を与えるだろうと思われる



特に重要な進展があったわけではないようだけど、1890年に、Joukowskiも自由流線理論に関する論文を書いている。

1907年には、イタリアのLevi-Civitaが、平板以外のcurved obstalceに適用可能な一般論を展開したとされている(多分、今井功『流体力学(前編)』§54にあるような内容だと思うけど嘘かもしれない)。Levi-Civitaの論文は、以下で読めるっぽいけど、(イタリア語が)読めない。Levi-Civitaといえば、「接続」の枕詞くらいの認識だけど、こういうこともやっていたらしい

Scie e leggi di resistenza [英訳:Trails and laws of resistance]
http://doi.org/10.1007/BF03013504



1923年になって、イギリスのBrodetskyが、円柱に対して、自由流線理論を適用した計算を発表した。

Discontinuous fluid motion past circular and elliptic cylinders
https://royalsocietypublishing.org/doi/10.1098/rspa.1923.0014

また、ドイツのCurt Schmiedenは、1929年、1932年、1934年に、同じく円柱に自由流線理論を適用して、論文を書いている。例によって、ドイツ語なので読めない
Die unstetige Strömung um einen Kreiszylinder
https://link.springer.com/article/10.1007/BF02079711

Über die Eindeutigkeit der Lösungen in der Theorie der unstetigen Strömungen
https://link.springer.com/article/10.1007%2FBF02080809

円柱の場合は、一般に解析的に解くことはできないけど、複素対数速度が、単位円板上で正則なので、そこでTaylor展開することができ、係数を数値的に決定できる。Schmiedenが得た面白い結論の一つとして、物理的に許される剥離点の剥離角(円柱前部のよどみ点から剥離点までの角度を円柱中心周りに測った大きさ)は、概ね55度〜125度の範囲にあるというのがある(らしい)。これらの角度の範囲外では、2つの自由流線が交わるということが起きる。実際の流れにおいて、どこで剥離するかは、Reynolds数に依存して異なるが、可能な流れは、ポテンシャル流の計算で、ある程度制限される。

これは、定常性を仮定した議論なので、剥離点の位置が時間的に変動する場合は、これらの限界を超える可能性はある。実験的に剥離位置を調べた結果は、
円柱を過ぎる流れの剥離
https://www.jstage.jst.go.jp/article/jjsass1969/20/226/20_226_610/_article/-char/ja/
の第10図に、レイノルズ数の範囲6.0e4〜5.0e6での剥離角の測定結果が載っている。レイノルズ数が3.5e5〜1.5e6では、剥離角が140度強に達しているけど、それより低い領域では80度前後、高い領域では120度程度と、Schmiedenの計算値内に留まっている。レイノルズ数が3.5e5〜1.5e6では、円柱に剥離泡が付着する(第11図の超臨界領域)らしく、そもそも、流れが、自由流線理論でモデル化されてるものとは異なる。


1933年に、ChaplyginとLaurentievは、平板上面真ん中で剥離する流れに働く揚力と抗力を計算したらしいが、論文が、どれか分からない。冒頭の論文の計算に近いものか、実質的に同じものかもしれない。冒頭の論文と同じ計算は、Schmiedenが1941年に行っている。

[NACAーTM-961] Flow around wings accompanied by separatioai of vortices
https://ntrs.nasa.gov/search.jsp?R=19930094455

Schmiedenの論文と冒頭の論文は、複素ポテンシャルの取り方に定数差があるけど、それ以外は、同じ。今井功『流体力学(前編)』式(54.1)に合わせて、定数項を0とするなら、
w = \dfrac{C}{2}(\zeta^{2} + \zeta^{-2}) - 2C \cos(\theta_S) (\zeta+\zeta^{-1})
となる(\zetaは、Schmiedenの論文では\tauになっている。それ以外の記号は、論文通り。冒頭の論文の記号では\theta_S=\sigma_0で、C=\dfrac{a^2}{2})。

そもそも(私の興味)は、Helmholtz流とKutta-Joukowski流を繋ぐ解があるなら面白いと思ったのだけど、残念ながら、そうはなってない。Schmiedenは、2つの極限状況を扱っていて、一つは、Helmholtz流になり、Helmholtz流から、前縁の剥離点を後端へ向かってう動かしていく途中で、2つの自由流線の交差が起きるようになるっぽく、それを、もうひとつの極限的ケースと位置づけている。つまり、迎角の大きさに応じて、上面途中の剥離点が動ける範囲が制限を受け、(迎角0度の場合を除いて)後端まで動かすことはできない。

数学的には、Schmiedenの論文に於けるk^2は、0を超えて、-1まで動くことができ、冒頭の論文では、「ただあまり剥離点を後緑近くにもつていくと,上下の剥離流線が交るようになると思われるが,そのときにもこの理論はなお近似的な意味は持ち得るであろう」として、さらっと、限界を超えているけど、Schmiedenは、自由流線が交差するべきでないという考えから、k^2は正としている。名前がないと不便なので、k^2=0の時の流れを、Schmieden流と呼んでおく

Schmieden流の場合は、(冒頭の論文では、より簡潔に、Poisson-Schwartzの積分公式で計算されている通り)
\dfrac{dz}{dw} = \dfrac{ 1+ \zeta^2 e^{-\alpha}}{1+\zeta^2 e^{i\alpha}}
なので、dz/d\zetaを決定できる。積分すると、z=z(\zeta)が求まる。Schmieden流に限らない一般の場合も、解析的に計算することができる。ついでに、Schmiedenの論文の式(3)の分母内に符号の誤植がある

Schmieden流では、迎角α>0の時には、上面途中で、剥離が生じている。迎角が10度の時、剥離位置は、後端から、L/5ほど進んだ所(Lは平板の長さ)にある。Helmholtz流でも揚力はあったけど、Schmieden流の場合は、標準的な揚力計算の結果と類似した力が出る。平板翼のSchmieden流に対する揚力係数は、迎角をαとした時
C_L = 2 \pi \sin(\alpha) \cdot f(\alpha)
の形で書ける。αが小さい時、f(α)は1より少しだけ小さい。αが10度の時、f(α)は、0.908で、通常の揚力計算によるより10%ほど小さい。

圧力抵抗は、複素対数速度をTaylor展開した一次の項の係数に比例する(今井功『流体力学(前編)』式(54.13)にある通り)ので、Schmieden流の圧力抗力係数は、剥離があるにも関わらず、0となる。


Schmiedenの論文冒頭には、以下のように書かれている。

The flow around wings computed by the usual method leads in the case of a finite trailing edge to a stagnation point in the trailing edge due to the Kutta-Joukowsky condition of flow governing this region. As a result, the theoretical pressure distribution differs substantially from the experimental values in the vicinity of the trailing edge.

Kutta条件を課して計算すると、後縁角が正の場合、後端の流速は0なので、後端近傍の圧力分布は、計算値と実験値が大きくずれると言っている。上の方であげた守屋富次郎の報告中の第10図に、NACA-4412翼型(迎角6.4度)に対する実験値と計算値が比較してあって、後端近くまで実験値がプロットしてあるけど、確かに合ってない

自由流線理論ならいいかというと、自由流線理論では、デフォルトの(Schmiedenの計算でも使われている)Kirchhoffの死水モデル(今井功『流体力学(前編)』§54)に従う限り、(平板翼に限らず)後端の流速は一様流速に等しくなるはずだけど、NACA-4412翼型の実験値を見ると、これも成立していなそう。これは、背圧を静圧と等しいとしているせいで、cavitation numberを決めれば解決するかもしれない

高レイノルズ数に於ける、平板に対する揚力係数の実験値が、意外と見つからなくて困るのだけど、最初の方に書いたように、かなり小さい迎え角でも剥離泡が形成されて、理論値とずれ始めるらしい(要出典)


とりあえず、Schmiedenの計算と標準的な揚力計算で、平板翼に対して、揚力係数が近いだけでなく、翼表面の流速分布が近いことも確認しておく。自由流線理論でも、死水域の外では、流速分布からベルヌーイの定理で、圧力分布を決めていい

標準的な揚力計算の結果は、今井功『流体力学(前編)』式(33.1)と(33.9)を使い(a=1/2とした)、自由流線理論の結果は、Schmiedenの論文の式(10)及び(12)を使う(zの積分定数は、zの範囲が、-1から+1になるように決定した)

横軸は、平板の位置座標(-1から+1の範囲。普通は、0〜1になるように取る)で、縦軸は、平板上の流速を一様流速で割った無次元量(守屋富次郎の報告内の式(14)で、\dfrac{v}{V}と書いてある量。裏と表の速度2つがある)。自由流線理論の計算は、途中で剥離が生じ、一部は、死水域に入っているので、そこの流速分布は決まらない

以下は迎角10度の時のグラフで、青が標準的な揚力計算から出る流速分布で、赤は自由流線理論から出る流速分布。異なる考えから出発して、式が全然違うにも関わらず、よく一致している。迎角を小さくすると、両者の区別が殆どつかなくなるので、多少は、差が見える値として、この迎角を選んだ。

f:id:m-a-o:20190824140147p:plain
Kutta-Joukowski流とSchmieden流の流速分布

自由流線理論の論文は、その後も出ているけど、実際の翼型に適用したという類の話は少ないように見える。

任意物体のまわりの自由流線理論
https://repository.exst.jaxa.jp/dspace/handle/a-is/24280

では、自由流線理論の新しいモデル(自由流線上で、流速は一定でなく、無限遠で一様流速に等しくなる。もはや定義上の"自由流線"じゃない)を提案し、数値計算法を与えている。シリンダーと(比較的迎角の大きめな)NACA4412翼型で、圧力分布を再現できたと書いているけど、剥離位置と背圧を、圧力分布から推定したと書いてあって、ただのパラメータフィッティングなので微妙。


自由流線理論を、現在の標準的な流体力学のカリキュラムで習うことは、まずないだろうけど、翼の揚力計算について無力で誤った雑魚理論というわけではない

コンピュータ以前の数値計算(1) 三角関数表小史

現代の三角関数計算

三角関数の値を計算する方法として、現代人が素朴に思いつくのは
(1)いくつかの角度に於ける値を事前に計算しておき、一般の場合は、それを補間した値を使う

(2)Taylor展開の有限項近似

の二つの方法だと思う。Taylor展開を使う場合、角度をラジアン単位に変換する必要があるので、円周率を、ある程度の精度で知っていないといけない。


コンピュータ用に、もう少し凝ったアルゴリズムが使われることもある/あったらしいけど、今のコンピュータでは、(2)の方法が使われることが多い。例えば、Android(で採用されているBionic libc)では、アーキテクチャ独立な実装は、単純なTaylor展開を利用するものになっている。

https://android.googlesource.com/platform/bionic/+/refs/heads/master/libm/upstream-freebsd/lib/msun/src/k_sin.c

【追記】コメントで指摘をいただいた。単純なTaylor展開で13次まで計算した場合、任意のx \in [-\pi/4,\pi/4]に対して、Taylorの定理から
\left| \sin(x) - \displaystyle \sum_{k=0}^{6} (-1)^k \dfrac{ x^{2k+1} }{(2k+1)!} \right|= \dfrac{\cos(\xi)}{15!} |x|^{15}
を満たす-\dfrac{\pi}{4} < \xi < \dfrac{\pi}{4}が存在するので、誤差は、ワーストケースで\dfrac{(\pi/4)^{15}}{15!} \approx 2.041 \times 10^{-14} < 2^{-45}より小さいけど、上ソースコードで使われてる係数だと、(コード中のコメントによれば)誤差は、もう少し小さい。最大誤差が倍精度浮動小数点数の計算機イプシロンより小さくなるように、多項式の次数が決められているのかもしれないけど、そうすると、13次までのTaylor展開では、少し精度が足りない


人間が手で計算していた時代には、(1)の方法で計算されていた。事前に計算された値は、三角関数表として利用可能になっている必要がある。べき級数に頼ることなく、計算しやすい三角関数の値は、等分点(360度の有理数倍)に於けるもので、それは、代数方程式の解となるから、(2)の方法に頼ることなく、数値的に計算できる。この場合、正弦値の計算は、本質的には、円に内接する正多角形の一辺の長さを計算するのと同等でもある。

19世紀に、チャールズ・バベッジが計画した階差機関は、人手で作られた数表(三角関数表や対数関数表)の誤りをなくしたいという動機があったとされている。階差機関は、多項式を自動で計算(し印字)できる機械として設計されていて、三角関数なども、(2)に基づいて計算することを想定していたのだろう。

天文学と三角法

現存する写本はないものの、紀元前2世紀のニカイア(当時は、ビテュニア王国という国に属していたはず)出身のヒッパルコスが、三角関数表の一種として、「弦の長さの表」を作っていたらしいことは、他の本などの記述から確実とされ、最古の三角関数表だったと考えられている。

ヒッパルコスの動機は天文学にあり、それ以後も、三角関数表は、多くの場合、天文学とセットで出てくる。測量術や航海術でも使われるようになったのは、大航海時代より以降のことらしい。新しい土地へ行くことが増えたり、遠洋航海が増えたためだろう。地理学や地図作成技術自体は、非常に古くからあり、経緯度を定義したのはヒッパルコスだとされ、地図の起源は、もっと古い。

三角関数表のあるところに天文学があるというのは正しいけど、天文学があっても、三角関数表がないことはある。

中国では、(おそらく紀元前から)円周率の正多角形近似による計算が行われていたにも関わらず、一般の角度に於ける三角関数の値を計算するという意識はなかったのか、三角関数表のようなものは殆ど見られない。中国で三角法が発展しなかったことは、正弦や余弦という用語が作られたのが、17世紀であることからも察せられる。中国でも、夏(BC1900~1600)の時代に、日食の予報ができず死刑になった人の話とかあるし、それは伝説としても、暦を作るのは重要な仕事だったので、天文学がなかったわけではない。

ともあれ、天文学に動機づけられないと、"三角関数"のような考え方が便利だとは、なかなか思わないものなのかもしれない。考えてみると、角度の概念は日常にもありふれてる気がするのに、一回転360度というのさえ、天文学の影響が見られる。中国では、長い間、一回転は、"365.25度"だったらしく、天文学の影響が、より明らか。

円周率が3.16だった時代(?)

三角関数表を作るのに必要な計算技術は、円周率の多角形近似と同じで、三角関数表と違って、円周率の多角形近似は、複数の地域で追求がされた。歴史上使われた円周率の近似値を見ていると、3や3.14…以外に、3.16に近い値が、いくつかあるのに気付く。

・リンドパピルス(BC1850~1650頃?):円の面積と半径の二乗の比が、256/81≒3.16049…
・紀元前150年頃のインド:√10≒3.1622
・西暦1世紀頃の中国:√10
・初期の和算書『塵劫記』(1627):説明なしに3.16を採用

単なる偶然かもしれないけど、24 \tan(7.5^{\circ}) = 3.1596599\cdotsなので、外接正24角形を使って近似計算した結果、出てきた数値なのかもしれない。仮にそうだとして、外接正24角形が頻出する理由が何かあったのか気になる。

内接正多角形より外接正多角形を好む理由として、"円周と直径の比=円の面積と半径の二乗の比"という事実が、容易に分かるということが考えられる。外接正多角形での近似を認めれば、"円周と直径の比"及び"円の面積と半径の二乗の比"は、同じ数列の極限
\pi = \lim_{n\to\infty} n \tan( \dfrac{180^{\circ}}{n} )
となって、等しいことは自明となる。内接正多角形での近似を使った場合は、2つの量は、異なる数列の極限になるので、極限値が等しいことは、自明じゃない

不思議なことに、ユークリッドの『原論』には、円の面積と直径の二乗が比例することは書かれている(12巻)のに、"円周と直径の比=円の面積と半径の二乗の比"であることは書かれてないらしく、一般的には、これは、アルキメデスの成果とされている。まぁ、『原論』は計算が殆ど出てこない特殊な本だし、また、小アジア〜地中海圏以外の地域の人にまで、アルキメデスの議論が伝播して理解されたと考えるのは、無理があるように思える。


文献上では、内接正多角形を使った近似値だけでなく、外接正12角形や外接正48角形を使ったと思われる円周率の近似値も、あまり見られないっぽい。
外接正12角形による近似計算→12 \tan(15^{\circ}) = 3.215390\cdots
外接正48角形による近似計算→48 \tan(3.75^{\circ}) = 3.1460862\cdots
外接正96角形による近似計算→96 \tan(1.875^{\circ}) = 3.14271459\cdots
で、外接正96角形は、アルキメデスが、円周率の上界の評価に用いたものでもあり、得られる値は、円周率の最良近似分数の一つ22/7に近い。

外接正24角形は、やっぱ特別らしい。考えられることとして、直径1の円に於いて、
外接正24角形の一辺の長さ→\tan(7.5^{\circ}) = \sqrt{6} - \sqrt{3} + \sqrt{2} - 2
外接正12角形の一辺の長さ→\tan(15^{\circ}) = 2 - \sqrt{3}
内接正10角形の一辺の長さ→\sin(18^{\circ}) = \dfrac{\sqrt{5} - 1}{4}
内接正12角形の一辺の長さ→\sin(15^{\circ}) = \dfrac{\sqrt{6} - \sqrt{2}}{4}
などとなって、一辺の長さが、正有理数の平方根の和の形になる場合に限れば、外接正24角形で近似精度が一番高くなるのが理由かもしれない。

平方根の計算については、バビロン第一王朝の頃(BC1830~BC1530)のバビロニアで、2の平方根を計算した粘土板"YBC 7289"があるらしい。YBC7289は、画像で検索するとわかるけど、正方形らしき絵と、3つの数字が書かれてるだけの単純なものらしい。3つの数字は、30と√2の近似値、30√2の近似値の3つで、一辺の長さが30の正方形の対角線の長さを表したものと考えられている。

YBC7289に書かれてる数字は、しばしば、単に60進法であると書かれてるけど、実際には、10進法と60進法が混在した表記法になっているようである。それはともかく、YBC7289に書かれている2の平方根の近似値は、60進法で、1;24 51 10= 1+24/60+51/3600+10/216000=30547/21600≒1.41421296296296...だそうで、まぁ数字しか書いてない以上、どんな方法を使ったか確実なことは分からないが、

Square Root Approximations in Old Babylonian Mathematics: YBC 7289 in Context
https://doi.org/10.1006/hmat.1998.2209

では、この数値は、最良近似分数\dfrac{577}{408} = 1 + \dfrac{24}{60} + \dfrac{51}{3600} + \dfrac{10}{216000} + \dfrac{1}{367200}から得たと推測している。

論文では、この近似値の計算に使った方法として、初期近似値a > 0を適当に選んだ時、B=a^2-2とすると、
\sqrt{2} \approx a - \dfrac{B}{2a}
によって、改善された近似値が得られるので、これを繰り返し使ったのだろうと推測している。


これは、現在、Babylonian methodと呼ばれるアルゴリズムと同じもので、現代では、Newton法の特殊形として説明されがちだけど、初等的に理解できる。実際、(a - \frac{B}{2a})^2 - 2 =\left( \frac{B}{2a} \right)^2なので、\left( \frac{B}{2a} \right)^2 < |B|ならば、a - \frac{B}{2a}はaより良い近似値である。

で、a^2<2の時は、\left(a - \frac{B}{2a} \right)^2>2になるので、結局、a^2>2の時だけ考えればいい。そして、a^2>2なら、B>0で、簡単な計算で、\left( \frac{B}{2a} \right)^2 < Bは、いつでも成り立つことが分かる

以上の議論から、求める近似精度を指定した時、初期近似値から何ステップで必要な近似値に到達するかを見積もることもできる。尤も、Babylonian methodは収束の早い有能なアルゴリズムなので、実用上は、単に近似値の二乗を計算して、近似の良さを評価すれば十分だったかもしれない。そして、a=3/2から始めると、次が、17/12で、その次に577/408を得る。Babylonian methodは、もしかしたら、Euclidのアルゴリズムより古い、最古のアルゴリズムかもしれない。エジプトでは、どうだったか調べてないけど、平方根の計算が、非常に古くから行われてた可能性はあるだろう。


Babylonian methodを使って、整数の平方根の最良近似分数を得られるけど、整数の平方根の最良近似分数には、分母と分子がペル方程式の整数解を与えるという見方もある。例えば、ここで使った√2の近似値の分子・分母は、ペル方程式x^2-2y^2=1の整数解になっている。

YBC7289より後の時代のものであり、また、バビロニアからの影響があったのかも不明であるけど、古代インドのシュルバ・スートラ(BC800~BC200)には、√2の近似値として、17/12と577/408が記載されているらしい。ペル方程式の解を得たなら、99/70が登場してもよさそうだけど、Babylonian methodを使ったなら、99/70がスキップされているのも説明が付く。古代のインド人が、どういう方法を使ったか詳細は知られてないようである。

Babylonian methodは、無理数の平方根も整数の平方根も同じように計算できるけど、古代の人が、整数や有理数の平方根の計算を好んで、無理数の平方根を避けたとしても、気持ちは理解できる。昔の人は、外接正24角形の辺長を首尾よく、正有理数の平方根の和で書くのに成功した後、外接正48角形でも、同様の結果を求めて試行錯誤したが果たされず、外接正24角形による円周率評価を暫定的に採用したのかもしれない。

仮に、Babylonian methodによって平方根を計算したとして、例えば、初期値1から僅か3ステップで、√2と√3の近似値577/408と97/56を得る。この近似値から外接正24角形の周長によって、円周率を概算すると
24 (\sqrt{2}\sqrt{3} - \sqrt{3} + \sqrt{2} - 2) \approx 177/56 = 3.160714285\cdots
となる。このくらいの計算は、古代の人にとっても、辛いものではなかったろう。


後に、アルキメデス(BC287~BC212)は、著書"Measurement of a Circle"の中で、説明なしに、√3は、265/153と1351/780の間にあるという事実を使用したらしい。アルキメデスが説明しなかったのは、単に二乗して3を引けば確認できると思ったのか、当時、よく知られた事実だったのか、それ以外の理由か分からないけど、分子と分母が、方程式x^2-3y^2=-2及びx^2-3y^2=1の解になっていることから、山勘で選んだ数値では、なさそうである。そして、1351/780は、Babylonian methodで得たのかもしれない(初期値として、x=5/3などを使うと得られる)けど、265/153は、真の値より小さいので、Babylonian methodで得たものではないだろう。

(\sqrt{D}を計算する)Babylonian methodは分数変換f(x) = \dfrac{x^2+D}{2x}を繰り返し適用する形になるけど、\sqrt{D}に収束する分数変換は無数にある。例えば、Babylonian methodは、Pell方程式の加法構造に対する倍角公式に相当するものとなっているけど、三倍角の公式として、f(x) = \dfrac{x^3 + 3Dx}{3x^2+D}などを使ってもいい。これは、Newton法から得られる変換ではないが、Babylonian methodより収束は速いはず。

収束は遅いが簡単な変換として、分子と分母が共に一次のf(x) = \dfrac{3+x}{1+x}を、x=1に繰り返し適用すれば、265/153と1351/780を得られる。アルキメデスは、これに類した変換を用いた可能性を提案した人もいるが、この変換を自然に思いつく筋道は分からない。

より自然に思いつきそうな方法として、0 \lt a^2 \lt 3 \lt b^2なる正数a,bに対して、線形補間
x=a + \dfrac{3-a^2}{b^2-a^2}(b-a) = a + \dfrac{3-a^2}{a+b}
を繰り返すことで、逐次的に、下限aを更新するという手もある。b=2と選べば、分数変換\dfrac{2x+3}{x+2}を繰り返し適用する形になり、更に、初期値をx=1にすると、1→5/3→19/11→71/41→265/153→…が順番に得られる。

Babylonian methodで上限を得て、線形補間で下限を得るというのは、割と一般性があるけど、所詮は憶測でしかない。とりあえず、エジプトやバビロニア、インド、古代ギリシャで、平方根の計算が、どれくらい一般性を持って理解されていたかは、よく分からないが、ある程度は計算する手段を持っていたようである


円周率の話に戻ると、外接正24角形による近似が本当に多用されたのかは分からないけど、以上のようなシナリオはありえないこととも思えないので、宇宙人や異世界人も、初期文明では、3.16に近い近似値を採用する可能性がある

古代オリエントの三角関数表

ヒッパルコス(BC190?~120?)以前に、三角関数表に類するものがなかったかは分からない。2017年に、バビロン第一王朝(紀元前19〜16世紀)時代のバビロニアに、"三角関数表"があったという論文が出ていた。

Plimpton 322 is Babylonian exact sexagesimal trigonometry
https://www.sciencedirect.com/science/article/pii/S0315086017300691

プリンプトン322は、4列15行の数値表で、4列目は行番号、1,2,3列は(\left( \dfrac{p^2+q^2}{2pq} \right)^2 , p^2-q^2 , p^2+q^2 )の形の数値で、1列目の大きさ順でソートされている。一列目は欠損があるので、\left( \dfrac{(p^2-q^2)}{2pq} \right)^2という解釈もできるらしいけど、どっちを選んでも、大きな影響はない。(p,q)は正整数の組で、一行目から順に、(12,5),(64,27),(75,32),(125,54),(9,4),(20,9),(54,25),(32,15),(25,12),(81,40),(60,30),(48,25),(15,8),(50,27),(9,5)とすると、表が再構成される。表は、60進表記で、各桁が、60の何乗に対応するのか不明らしい。例えば、11行目の2,3列目は、(45,75)かもしれないけど、それぞれを60倍した(2700,4500)と解釈されている。

ということは以前から分かっていたけど、これらの組を選んだ基準とか、この表の目的については、共通見解がない。

論文では、de Solla Priceの1964年の提案通り、38行目まで続きがあったとして解釈をしている。(2pq , p^2-q^2,p^2+q^2)は、ピタゴラス数なので、表は、直角三角形のリストで、鋭角の大きさに従って、ソートされているとも解釈できる。角度の分布は、残っている15行目までだと、45度弱〜32度程度だけど、38行目まで補うと、最小角は2.34度弱となる。表には、12709と18541のような大きな数が含まれているので、バビロニア人が、原始ピタゴラス数(12709,13500,18541)を作り出す方法を知ってたことは、間違いないと思われる

論文には、表の使い方とかについても書いてあるけど、仮に、主張が完全に正しくても、通常の意味での三角関数表とは違って、三辺の長さが整数比という縛りがあるので、等分点に於ける弦長や正弦値を計算しているようなものではない。なので、"三角関数表"と呼ぶのは、語弊が大きい。

ピタゴラス数やペル方程式は、初等整数論に於ける主要なテーマだけど、元々の動機は、"応用数学"にあると言えるのかもしれない。数論には最近まで何の応用もなかったと言われることもある気がするけど、単に人類が、その起源を忘れてるだけだろう。



バビロニアは、バビロン第一王朝以後も、長い間、少なくとも天文学では、先進地域であり続けた。当時、天文学と占星術は結びついていて、ヘレニズム時代になると、バビロニア占星術が伝わった結果、ホロスコープ占星術として、アレキサンドリアで発展したのは、その表れと言える。バビロニアの天文記録は、現存する一番新しいものでは、西暦74〜75年のもので、楔形文字記録の最後のものでもある。

紀元前2世紀に作られた"アンティキティラの機械"で採用されている、System Bなるルールがあるらしいけど、これは、バビロニア由来のものと思われている。紀元前4世紀の人であるKidinnuが考えたという説があり、ギリシャに紹介したのはヒッパルコスであるかもしれない。ヒッパルコスの知識の内、どれがバビロニア由来のものかは明らかではない

ヒッパルコスの表は、7.5度刻みだったとされている。これは、内接正48角形の一辺の長さを計算できれば十分。ヒッパルコスの表の値は、現代の記号では、2 \sin(\theta/2)を計算したものなので、3.75度刻みで正弦値を計算したのと同等。

3.75度は、30度の1/8なので、30度の正弦値から始めて、15度、7.5度、3.75度の正弦値を計算していけばいい。これくらいの刻み幅でも線形補間した時の精度は、それほど悪いものではない。3.75度と7.5度の正弦値から5度に於ける値を線形補間で計算した場合、0.08711081689…となり、5度の正弦値は、0.087155742…で、誤差は0.1％より小さい


少し後の時代になって、AD2世紀に、アレキサンドリアのプトレマイオス(83年頃〜168年頃)が書いたとされる天文学書『アルマゲスト』に掲載されている「弦長の表」は、現代まで写本が伝わっていて、0.5度刻みになっているらしい。

Ptolemy's table of chords
https://en.wikipedia.org/wiki/Ptolemy%27s_table_of_chords

アルマゲストの表を作るには、0.25度における正弦値が必要だけど、30度や90度に於ける正弦値から始めて、二等分していくだけでは、この値を知ることはできない。

計算方法は、色んなところで説明されているけど、基本的な方針は、既知の値から始めて線形補間が十分な精度となるまで二等分を繰り返し、最後に線形補間によって、0.5度に於ける弦長(0.25度の正弦値の2倍)を決定したらしい。出発点には、12度に於ける弦長を使ったらしい。正五角形の一辺の長さは、72度に於ける弦長であり、これと、60度に於ける弦長と合わせて、加法公式から、12度に於ける弦長が決まる。後は、二等分を繰り返して得られる、12/16度と12/32度に於ける弦長を線形補間して、0.5度の弦長を決定できる。プトレマイオスは、この表を使って線形補間するように書いているらしい。

ヘレニズム文明圏の書写材料はパピルスで、紀元前2世紀頃、アナトリアのペルガモン王国で、羊皮紙が量産されるようになったと伝えられる。

プトレマイオスは、占星術書『テトラビブロス』も書き、これが後の西洋占星術の基礎になったらしい

古代オリエント→インド

メソポタミア地域とインド地域の交流は、非常に古くからあって、シュメール人とインダス文明の時代には既に交易を行っていたと考えられている。学術的な交流がどれくらいあったのか分からないけど、ヒッパルコス以降のある時期に、インドに、三角法が伝播したと推測されている。古代バビロニア起原とされている黄道12宮や曜日なども、オリエント地域に広まっていたものが、AD3世紀頃、インドに伝わったとされており、同時期に、伝来したものかもしれないけど、証拠はない。

紀元前後、仏教とギリシャ文化は、パルティア、バクトリア、ガンダーラ地方や中央アジア方面で共存してたし、紀元1世紀にはインド洋で季節風貿易が行われてたので、どこで、どういう形で伝わっても不思議はないけど、正確な時期や伝来経路は、よく分かってない。

おそらく、インドには、『アルマゲスト』より前の知識しか伝わらなかったと見られている(知られる限り、『アルマゲスト』のサンスクリット語翻訳は、18世紀に、Jagannatha Samratによって、アラビア語版をベースとして、なされたらしい)。


4世紀後半〜5世紀初期に書かれたと推測されている天文学書『スーリヤ・シッダーンタ』には、三角法と天文学への応用が書かれていたようである。この本は、ヘレニズム数学で見られなかったsinとcosと等価な概念を使っているらしい。1860年に英訳されたヴァージョンが、以下で読めるよう(長いので、読んでないけど)

Translation of the Sûrya-Siddhânta
https://books.google.co.jp/books?id=jpE7AAAAcAAJ

紀元500年頃、インドの数学者・天文学者アーリヤバタは、『アーリヤバティーヤ』という本を書いて、これの内容は、現在まで残ってるらしい。アーリヤバタは、パータリプトラにあったナーランダー僧院の学長を務め、ナーランダー僧院には、大きな天体観測所があったとWikipediaには書いてある。ナーランダー僧院は、当時最大の仏教の学院で、少し後の時代には、玄奘三蔵も、636〜641年まで、ここに滞在した。

『アーリヤバティーヤ』では、3.75度刻みの正弦値を記した表が載ってるらしい

Āryabhaṭa's sine table
https://en.wikipedia.org/wiki/%C4%80ryabha%E1%B9%ADa%27s_sine_table

3.75度刻みなので、多分、ヒッパルコスと同じような方法で計算したと推測される。プトレマイオスは、円周率を377/120=3.1416666...としたらしいけど、アーリヤバタは、62832/20000=3.1416を採用したと書いてある。外接正384角形の周長から評価した場合、3.141662747…となり、内接正384角形の周長を使うと、3.1415576079…となり、アーリヤバタは、後者の数値の近似として、3.1416を採用したらしい。円周率はともかくとして、基本的には、この時代のインドに於ける三角法は、『アルマゲスト』より、大きく優れてる面は、ないっぽい。


紀元7世紀には、紀元前から存在する都市ウッジャインの天文台の天文台長だったらしいブラフマグプタ(598〜668)はPell方程式を調べていて、恒等式
(x_1^2-Dy_1^2)(x_2^2-Dy_2^2) = (x_1x_2+Dy_1y_2)^2 - D(x_1y_2 + x_2y_1)^2
を発見したとされている。これは、今日、Brahmaguptaの恒等式と呼ばれる。これは、加法定理でもあるけど、ブラフマグプタが三角関数と結びつけて考えたかは分からない。

ブラフマグプタは、他にもブラフマグプタの補間公式という二次の補間法で知られる。ブラフマグプタの頃には、0を用いた十進記数法が完成していたようである。


北インドでは、550年にグプタ朝が滅び、中心都市であったパータリプトラは衰退したが、滅んだわけではなく、ナーランダー僧院も1193年まで残っていたようである。

古代インドの書写材料には、貝葉という、ヤシの葉を加工したものを使っていたらしい。インドへの紙の伝来は、イスラム世界によって12世紀頃、もたらされたとされている


インド→中国

中国では、3世紀頃には、正192角形や正3072角形の周長から、円周率を評価していたらしいから、正弦の特殊値の計算として見れば、プトレマイオスのものより細かい計算ができていたことになる。概念的な面では、三角法には繋がっていないっぽい。


中国には、古くから、土圭之法とか、圭表という日時計の一種があって、冬至を知るのに利用され、周代には存在していたとも言われるけど、一日の時刻を知るのに使われたかは分からない。

『九章算術』訳注稿 (1)
http://pal.las.osaka-sandai.ac.jp/~suanshu/j/publications2.html

によると、AD263年に劉徽が注釈を作成した「九章算術」には、"周官大司徒職、夏至日中立八尺之表。其景尺有五寸、謂之地中。説云、南戴日下萬五千里。"(『周官』大司徒に「夏至の日の南中時、８尺の晷針を立て、その影が１尺５寸になる地を「地中」と謂う」と。（鄭玄の）説に「そこは、（夏至の南中時に）太陽が真上にくる地点より１万5000里離れている」)という記述があるらしい。

これも、圭表の記述に相当するものと思われ、"八尺之表"とは
表 (道具)
https://ja.wikipedia.org/wiki/%E8%A1%A8_(%E9%81%93%E5%85%B7)
のことだろう。

"８尺の晷針を立て、その影が１尺５寸になる地"は、北緯34度あたりで洛陽や長安のある緯度に近い。夏至の南中時に太陽が真上にくる地点とは、今で言う北回帰線(北緯23.4度)で、南越国とかあったあたりまで南下すれば、確認できたはずだけど、実際に行って測定したかは定かでない。

上記の記述の後に説明があって、(大地が平坦と仮定して)洛陽付近の南北二点間に於ける、同じ長さの棒の影の長さを測定して、これと二地点間の距離に基づき、連立方程式を解くことで、太陽の高さ、及び北回帰線と"北緯34度線"(彼らのいう"地中")の距離を決定したっぽい。

一旦、古代中国人の方法で"太陽の高さ"が既知(上の記述では、夏至の南中時には、高さ8万里にあるという想定らしい)になれば、夏至の南中時に影の長さを測定するだけで、他の地点でも、北回帰線との距離が決定できる。この計算は、ある意味では、三角法と言えなくもないけど、三角関数表は全く必要ない。

エラトステネスと違って、結果的には、古代中国では、誤った仮定に基づいて計算していたわけで、太陽と地球の距離に関しては大きな差が出たけれど、地上での距離計測に関して言えば、古代中国人の生活圏では、十分実用的で、実際に二地点間の距離を測定して、自分たちの計算の正しさへの確信を深めた可能性さえある。

「地中」と北回帰線の距離は、1200km弱で、これが一万五千里だと言ってるから、一里80mくらいの換算になる。普通は、一里4〜500mくらいと考えられているけど、こうした計算があることは、魏志倭人伝の解釈で使われることがある短里説(一里75〜90m)の根拠とされている。



紀元718年に、インド人を祖先に持つとされる瞿曇悉達は、唐で『開元占経』を編纂し、これの104巻には、位取り記数法の説明とかが書いてあり、この中にアーリヤバタの正弦表も含まれている。『開元占経』は、天文・暦学・占術学の本とされ、冒頭は、古代に於ける宇宙論のような内容を含む。

『開元占経』は、写本が沢山残っているらしく、検索すると、いくつか見つかる。raw textと画像が、

中國哲學書電子化計劃:《開元占經》
https://ctext.org/wiki.pl?if=gb&res=348345

大唐開元占經 殘三卷
http://kanji.zinbun.kyoto-u.ac.jp/db-machine/toho/html/C004menu.html

にある。冒頭の"算字法：樣一字、二字、三字、四字、五字、六字、七字、八字、九字點，右天竺算法，用上件九個字，乘除其字，皆一舉禮而成。..."とか書いてある部分(と、その続き)が、位取り記数法の説明っぽい(?)。画像の方で見ると、この部分には、算木数字が書かれている

算木数字
https://ja.wikipedia.org/wiki/%E7%AE%97%E6%9C%A8#%E7%AE%97%E6%9C%A8%E6%95%B0%E5%AD%97

正弦表は、"推月間量命段法：凡一段，管三度四十五分，每八段管一相，總有二十四段，用管三相。其段下側注者，是積段，並成三數。第一段，二百二十五。第二段，二百二十四，並四百四十九。第一相；第三段，二百二十二，六百七十一。(中略)第二十四段。七，並三千四百三十八。"のように記述されている。

これは、3.75度ごとの正弦値(の3438倍)に相当するものを表しているけど、例えば、"第二段，二百二十四，並四百四十九"。の449が正弦値3438 \sin(7.5^{\circ}) = 448.7490\cdotsに相当するもので、224は、第一段の数値225との差分を表す。


725年頃、大衍暦の作成を命じられた、唐代の僧である一行は、tangent表を作成したらしい

AN EIGHTH CENTURY CHINESE TABLE OF TANGENTS
https://www.jstor.org/stable/43290348?seq=1#page_scan_tab_contents

『続日本紀』には、天平7年(735)、吉備真備が唐から持ち帰ってきたものの中に、大衍暦経一巻、大衍暦立成十二巻、測影鉄尺一枚、...と書かれている。この時に、日本にも、正接表が持ち込まれた可能性はある。測影鉄尺は詳細がよく分からないけど、冬至の影を測る鉄の棒などと解釈されてることが多い。圭表と同じものなのかもしれない。

これと前後して、日本では、陰陽道、天文道、暦道が成立して、これらの技術は、江戸時代まで国家の管理下にあり、秘匿されていた。


世界最初のTAN表の制作方法
http://www.osaka-kyoiku.ac.jp/~jochi/j18.htm

では、一回転を364"度"として、実測によって、表を作ったのではないかと考察をしている。そうだとして、当時、『開元占経』で、インド式として、一周360度が紹介されてるのに、中国人が、頑なに360を採用しなかった理由は謎である。

364は7の倍数ということから、時々、魅力を感じる人もいるようで、一年364日の暦が存在したこともあるらしい(Qumran calendar,Enoch calendar)し、現代でも、一年364日で閏週で調整する暦を作ろうという提案もあったりするよう

数学史研究(通巻153号) 一行の正接関数表(724AD)
http://www.wasan.earth.linkclub.com/sugakusipdf/153.pdf

には、宣明暦でも、一行の表が踏襲されたと書いてある。宣明暦は、江戸時代に改暦されるまで、日本で、長期に渡って用いられていた暦。


これ以後、清代に、ヨーロッパ人がやってくるまで、三角関数表が中国で積極的に活用された例は、知られていない。圭表は、これ以後の中国でも使われていたようなので、正接表は使われていても、不思議はないけれど


インド→アラビア

ローマ帝国末期には、各都市で、非キリスト教系の施設が閉鎖・破壊され、異教徒は殺されたり追放された(アレクサンドリア図書館は、紀元400年頃、破壊され、アテネのアカデメイアも、紀元529年に閉鎖された)ため、多くの学者が、亡命先としてササン朝へ移動したと考えられている。ササン朝の学術中心は、ジュンディーシャープールだったらしい。

また、ササン朝では、ビザンツ帝国やインド、唐など各国の書物を集め、パフラヴィー語に翻訳したとされる。ササン朝は651年にイスラム教徒に征服されて滅亡した。皇族は、唐に亡命したらしいけど、首都クテシフォンの人口は、維持されたようだし、ジュンディーシャープールの学院は、832年にバグダードで設立された知恵の館と競合したと言われるので、その後も、200年以上、学術の中心地であり続けたようだ。こうして、ササン朝の技術と科学が、後のイスラム科学の基礎となったと考えられている。しかし、歴史書を見ても、その詳細は分からない


8世紀には、アッバース朝のアル・ファザーリが、インドの数学書、天文学書を、アラビア語翻訳して、『シンドヒンド』と呼ばれる本に、まとめた。中国と異なり、アラビアの方では、インドの数学や天文学を継承して発展させた。825年には、アル・フワーリズミーが『インドの数の計算法』（Kitāb al-Jām'a wa'l-Tafrīq bi'l-Hisāb al-Hindī)を書いて、この中には、インド式の十進記数法や三角法が含まれるらしい。

当時のインドでは、まだ球面三角法はなかったけど、ヘレニズム数学の成果を継承したイスラム世界では、実用的な球面三角法が発展した(アレキサンドリアのメネラウスが、球面幾何学の創始者とされている)。8〜12世紀のイスラム世界で起こったことの詳細は、様々な本で書かれているので省略。



第4代モンゴル帝国皇帝モンケの時代に、弟のクビライは中国地域の征服を担当し、三弟のフレグは西アジアの征服を担当して、それぞれ、後に、元とイルハン朝の創始者となった。フレグは、1258年に、バクダードを征服して、この時、大量の本が失われたと伝えられている。イスラム世界の中心地は、カイロに移る一方で、モンゴル帝国も、イスラムの科学者を連行し、その知識を継承・発展させようと試みている。

フレグは、1259年には、中央アジアのマラーゲ(現在のイラン東部)に、マラーゲ天文台を建設させ、イスラムの学者を連れてきて、研究させたようである。マラーゲ天文台で働いた人々は、マラーゲ学派と呼ばれる

元では、1271年、北京に回回天文台(イスラム天文台)が作られ、初代天文台長には、ジャマールッディーンという人が任命された。ジャマールッディーンも、それ以前はフレグに仕えていた人とされる。この頃の中国には、イスラムの数学・科学が、かなり持ち込まれた。元代に、イスラム圏の学術書が中国語翻訳されたという話は、聞かないけど、郭守敬は授時暦を作るに当たって、イスラム天文学の観測機器を利用したと言われる（具体的に、何を使ったのかは知らないけど)。

クビライは、ヨーロッパの科学に精通した人も集めようとしていたらしい。流石に、ヨーロッパは遠いので、ヨーロッパ人は、あんまり行かなかったようだけど。なので、マルコ・ポーロは有名人になった。少し後に、(ヨーロッパではないけど、中国までの距離は同じ)モロッコから、はるばる泉州、北京までやってきたイブン・バトゥータ(1304~1368)のような人もいる

少し後になって、中央アジアには、モンゴル帝国の継承政権の一つであるティムール朝が興り、首都サマルカンドには、1420年代に、ウルグ・ベク天文台が建設された。ウルグ・ベクはティムール朝第四代君主であるけど、当人も、天文学や暦学の研究を行ったらしい。

アル＝カーシー(1380〜1429)は、ウルグ・ベクに招かれて、サマルカンドを中心に活動したとされる。彼の本には、1度の正弦値を求めるのに、3度の正弦値から、三次方程式を使って計算する方法が書かれているらしい。また、本当かどうか知らないけど、フランスでは、余弦定理を「アル・カーシーの定理」と呼ぶと、Wikipediaに書いてある。

アル=カーシーは多角形近似の計算を推し進め、1424年の『円周論』で、円周率を高い精度で計算したらしい。アル=カーシーは60進数表記を使っているが、10進表記だと、3.1415926535897932…くらいまで合ってる計算になるよう。アル=カーシーは、別に趣味で、この計算をしたわけではなく、高精度の円周率が天文学で必要だと考えたのだそうだ


インド数学と三角関数のべき級数展開

インドでは、12世紀に解析学の始まりが見られる。バースカラ2世の『シッダーンタ・シローマニ』(1150)に、三角関数の微分を含む解析学の萌芽が見られるとされる。ヘレニズム数学にはなかったsinとcosを導入しておいたことが、役立った。バースカラ2世は、インドで球面三角法を導入した人でもある

バースカラ2世は、ウッジャインの天文台の天文台長だったらしい。

アル・カーシーと同時代のインドでは、マーダヴァ(1340 or 1350~1425)という人が現れ、ケーララ学派と呼ばれる数学と天文学の学派の創始者と伝えられている。ケーララ州は、インド南西部の一地方で、それ以前のインド数学の中心は、もっと北部にあったけど、多分、イスラム勢力が南下してきたため、Hindu数学の中心地は、南インドの方に移動したのだろう

ケーララ州には、コーリコード(カリカット)を中心とする王国や、コーチン王国などがあり、彼らは、この地方のみで使われるマラヤーラム語を話していたらしい。この時代の南インドには、Hindu系の大国ヴィジャヤナガル王国(1336〜1649)があり、関係がよく分からない。属国の類かもしれないけど、コーチン王国には、1409年に、明の鄭和が訪れ、明の保護国となっている。また、1500年に、ポルトガルの第2回インド遠征隊は、コーチン王国で歓迎され、1503年から1663年まで、ポルトガルの同盟国となった

ある人口の推定では、首都ヴィジャヤナガルは、1400〜1550年頃、全てのヨーロッパ都市とカイロを超える人口を擁する大都市であった。ヴィジャヤナガルの最盛期と、ケーララ学派が活躍した時期は、一致してるので、無関係ではないだろうと思う


マーダヴァは、三角関数のテイラー展開や、円周率のライプニッツの公式を導いていたとされていて、また、Taylor級数のtrunctionを使って、三角関数表を作成したと信じられている。

Madhava's sine table
https://en.wikipedia.org/wiki/Madhava%27s_sine_table

1530年頃までに、ケーララ学派が得た成果の多くは、『ユクティバーサ』という本に(証明付きで)まとめられ、世界初の微積分学の教科書と評される。実際には、微分については、大きな発展はなかったようで、速度が位置の時間微分であるという程度の認識はあったようだけど、微積分学の基本定理には到達しなかったっぽい。この本は、サンスクリットではなく、マラヤーラム語で書かれているらしい。どっちにしろ、読めないことには変わりないので、解説を見る。

Development of Calculus in India
https://link.springer.com/chapter/10.1007/978-93-86279-49-1_8
[PDF] http://www.ms.uky.edu/~sohum/ma330/sp12/india_calculus.pdf

解説も長いし、幾何学的議論は追うのが怠いけど、現代の視点から見ると、ケーララ学派は、積分を長方形近似で評価して極限を取ることで、多くの解析的結果を得たようだ。

基本的なところでは、x^nの積分を、
\displaystyle \int_{0}^{t} x^n dx = \lim_{k \to \infty} \dfrac{t}{k} \displaystyle \sum_{i=1}^k \left(\dfrac{i t}{k}\right)^n
によって計算したらしい。後に、ヨーロッパでも、同様の計算は、行われたようである(FermatやFaulhaberなど)

π/4の級数展開は、1/(1+x^2)の級数展開を項別積分するのと等価な式を示すことによって得た(上記解説中の式(124)など)

sin(x)の級数展開については、上記解説中の式(169)(170)がキーになる式だけど、これらの式は、以下の2つの積分
1 - \cos(x) = \displaystyle \int_{0}^{x} \sin(\theta) d\theta

\sin(x) = x - \displaystyle \int_{0}^{x} du \displaystyle \int_{0}^{u} \sin(t)dt

に対応するものと考えることができる。後者の積分は、両辺にsin関数が入っているので、積分を繰り返すことにより、冪級数展開の高次の項が決定される。

やってることは、Picardの逐次近似に近いけど、微積分学の基本定理を持ってなかったケーララ学派に、何らかの一般論があったわけではないと思われる。ケーララ学派では、上記2つの式を、(現代的に解釈すれば)、積分の長方形近似で、直接計算して得たようである。例えば、前者の積分を長方形近似で計算する場合、ちょっと頑張れば
\displaystyle \sum_{k=1}^{n} \sin(\dfrac{k x}{n}) = \dfrac{\sin(\dfrac{x}{2})^2 \cos(\dfrac{x}{2n})}{\sin(\dfrac{x}{2n})} + \sin(\dfrac{x}{2})\cos(\dfrac{x}{2})
を示すことができ、両辺にx/nを掛けてn \to \inftyの極限を取れば、求める積分を遂行できる。cos関数について、同様の計算をやれば後者の"sin関数に対する積分方程式"を証明することができる



こうして得られた冪級数を使って三角関数表を作るためには、円周率を、良い精度で計算しておく必要がある。マーダヴァは
\dfrac{\pi}{4} = 1 - \dfrac{1}{3} + \dfrac{1}{5} - \dfrac{1}{7} + \cdots
を証明したと考えられているけど、そのまま計算すると収束は遅い。上の解説によれば、『ユクティバーサ』には、初等的変形で得られる、もう少し効率のいい級数が書いてあるらしい。

具体的には
\dfrac{\pi}{4} = (1 - \dfrac{1}{a_1}) + (\dfrac{1}{a_1} + \dfrac{1}{a_3} - \dfrac{1}{3}) - (\dfrac{1}{a_3} + \dfrac{1}{a_5} - \dfrac{1}{5}) + (\dfrac{1}{a_5} + \dfrac{1}{a_7} - \dfrac{1}{7}) - \cdots
なので、
E(n) = \dfrac{1}{a_{n-2}} + \dfrac{1}{a_n} - \dfrac{1}{n}
とおけば
\dfrac{\pi}{4} = (1 - \dfrac{1}{a_1}) + E(3) - E(5) + E(7) - \cdots
という級数に変形できる。

(1 - \dfrac{1}{a_1}) + E(3) - E(5) + E(7) - \cdots \pm E(p) = (1 - \dfrac{1}{3} + \cdots \pm \dfrac{1}{p}) \mp \dfrac{1}{a_p}
だから、この変形は、\displaystyle \lim_{n \to \infty} \dfrac{1}{a_n} = 0であれば正しく、a_nの選び方によっては、級数を有限項で打ち切った時の誤差を小さくすることができる。

適用例として
a_n = (2n+2) + \dfrac{4}{2n+2}
a_n = (2n+2)
a_n = 2n
を使って
\dfrac{\pi}{16} = \dfrac{1}{5} - \dfrac{1}{3^5 + 4 \cdot 3} + \dfrac{1}{5^5 + 4 \cdot 5} - \dfrac{1}{7^5 + 4 \cdot 7} + \cdots
\dfrac{\pi}{4} = \dfrac{3}{4} + \dfrac{1}{3^3-3} - \dfrac{1}{5^3-5} + \dfrac{1}{7^3-7} - \cdots
\dfrac{\pi}{4} = \dfrac{1}{2} + \dfrac{1}{2^2-1} - \dfrac{1}{4^2-1} + \dfrac{1}{6^2-1} + \cdots
などが得られる。『ユクティバーサ』には、よりよい補正項として
a_n = (2n+2)+\dfrac{4}{2n+2+16/(2n+2)}
と同値な式が書かれているらしい。


【注釈】解説PDFでも注意されている(57ページ脚注)ように、円周率の"Leibniz級数"を有限項で打ち切った時の誤差項は、連分数展開によって厳密に書け、上のa_nは、誤差項の連分数展開を途中で打ち切って得られる。ところで、E_nをEuler数とする時、形式的べき級数間の等式として、以下が成立し、
\displaystyle \sum_{n=0}^{\infty} E_{2n} z^{2n} = \dfrac{1}{1 - \dfrac{z^2}{1 - \dfrac{(2z)^2}{1-\dfrac{(3z)^2}{1-\cdots}}}}
z = \dfrac{2\sqrt{-1}}{2n+2}とおけば、この形式的べき級数と、上記誤差項との関係は明らか。つまり、Leibniz級数の誤差項は、良い漸近展開を持つ。この漸近展開は、例えば、以下の論文に載っている。
Continued Fractions of Tails of Hypergeometric Series
https://doi.org/10.1080/00029890.2005.11920220

Many Correct Digits of π, Revisited
https://doi.org/10.1080/00029890.1997.11990646

誤差項は、
\displaystyle \int_{0}^{1} \dfrac{t^{a}}{1+t^2} dt = \dfrac{1}{2} \left( \dfrac{1}{a+1} + \dfrac{1!}{(a+1)(a+3)} + \dfrac{2!}{(a+1)(a+3)(a+5)} + \cdots \right)
のような形でも評価でき、実際上は、どれを使っても、大差なさそうに思う。この級数の証明は
I(a,b) = \displaystyle \int_{0}^{1} \dfrac{t^{a}}{(1+t^2)^{b}} dt
に対して、部分積分によって
I(a,b) = \dfrac{a+1}{2^b} + \dfrac{2b}{a+1}I(a+2,b+1)
を示せばいい。級数の収束も証明は難しくない。特に、a=0の時
\dfrac{\pi}{2} = \displaystyle \sum_{n=0}^{\infty} \dfrac{n!}{(2n+1)!!}
を得る(この級数は、少なくともEulerによって知られていたようである)。この級数の最初の10項を評価すると、1.5702…を得るので、円周率が、3.14より大きいことが分かる。一方、a=2として、最初の6項を足したものをライプニッツ級数の初項のみの評価値である1から引くと、0.78570…で、円周率に対する評価としては、22/7より少しいい。外接正96角形による近似計算に勝つには、7項まで評価しないといけないけど、計算量は大分少なくて済む。


ケーララ学派では、誤差項の式については、経験的に得られただけのものだった可能性が高く、また、マーダヴァが計算した円周率は、同時代のアル=カーシーの計算に精度では劣っているものの、多角形近似によらない点で、方法としては新しい。



天文学の方の成果について見ると、ケーララ学派のニーラカンタ(1444~1544)は『タントラサングラハ』(1501)を(サンスクリットで)書き、Wikipediaには、"Nilakantha's system was more accurate at predicting the heliocentric motions of the interior than the later Tychonic and Copernican models, and remained the most accurate until the 17th century when Johannes Kepler reformed the computation for the interior planets in much the same way Nilakantha did."と書かれている。彼のモデルは、地動説に基づくだけでなく、惑星の軌道が楕円であることを含んでいたとされてるけど、どういうモデルだったのか、詳細は知らない

【読んでない参考文献】
Modification of the earlier Indian planetary theory by the Kerala astronomers (c. 1500 AD) and the implied heliocentric picture of planetary motion
https://www.jstor.org/stable/24098820?seq=1#page_scan_tab_contents

Model of planetary motion in the works of Kerala astronomers
http://adsabs.harvard.edu/full/1998BASI...26...11R

予測精度の観点からすると、地動説か天動説かより、円軌道か楕円軌道かの方が重要ではある。ケーララ学派について書かれた資料を読んでいても、観測の話が出てこないけど、彼らが、観測を重んじなかったのかはわからない。ヒンドゥ系の天文学にも、14世紀後半に、イスラム世界から、アストロラーベが伝わったと言われるけど、そういう観測天文学系の話を読んでいても、ケーララ学派の話は全く出てこないので、ケーララ学派が、どういう立場にあったのか掴めない


ケーララ学派の数学がヨーロッパに伝わったという可能性は

TRANSMISSION OF THE CALCULUS FROM KERALA TO EUROPE
http://ckraju.net/Joseph/PA-3-Manchester-2007-paper.pdf

で、色々と考察がされているけど、決定的な証拠はない。

アラビア→ヨーロッパ

ヨーロッパでは、カスティーリャ王国が、1085年に、トレドを征服し、トレド翻訳学派と呼ばれる集団が形成され、アラビア語文献のラテン語翻訳(後には、カスティーリャ語翻訳)が行われるようになった。1000年頃のイスラム世界の中心地は、コルドバ、バクダード、カイロにあった。とある推計によれば、この三都市の中で、1200年頃までに人口を伸ばしたのはカイロのみで、コルドバは、1236年に、カスティーリャ王国に征服された。

神聖ローマ皇帝フリードリヒ2世(1194〜1250)は、プトレマイオスの「アルマゲスト」のラテン語訳を支援し、フリードリヒ2世の宮殿には、イスラムの学者も多く滞在していたと言われる。

この頃のヨーロッパの詳細は、それなりに分かっているようだけど、基礎科学に関して、他の地域で見られなかった発展を開始するのは、概ね、1600年頃からと言える。


一方、バグダードも、1258年に、モンゴル帝国に征服され、中央アジア〜東アジアでも、モンゴルの継承政権の元で、イスラム科学は暫く存続していたようだけど、サマルカンドのウルグ・ベク天文台が、1449年に破壊されて以降は、東アジア寄りの地域でのイスラム科学は消滅していった。サマルカンド出身の天文学者Ali Qushjiは、ウルグ・ベクの死後、1470年には、イスタンブールに移り、1474年に、そこで死んだそうである。およそ100年近く後のイスタンブールでは、天文台が建設されたものの数年で破壊されたとなっている。

Constantinople Observatory of Taqi ad-Din
https://en.wikipedia.org/wiki/Constantinople_Observatory_of_Taqi_ad-Din

天文台の建設提案者だったTaqi ad-Din(1526〜1585)は、Taqi al-Dinと綴られてることもある。ティコ・ブラーエ(1546〜1601)の同時代人なので、よく比較されるらしい。この頃でも、イスラム科学は、まだヨーロッパ科学の後塵を拝していたわけではない。

Taqi ad-jinの足跡を見ると、当時のイスラム世界の学術中心は、イスタンブール、カイロ、ダマスカスなどにあったと推測される。13〜15世紀頃のマラーゲ学派やウルグ・ベク天文台で得られた成果も継承されており、それは、ヨーロッパにも伝わったようである。

この頃、コペルニクスの弟子であるレティクス(1514-1574)は、10秒(1/360度)刻みの三角関数表を作ろうと試みたらしい。アルマゲストと比べても、随分細かくなっていて、観測精度や、測定精度に対する要求が向上したのかもしれない

円周率については、ドイツのLudolph van Ceulenという人が、正多角形近似に基づいて、1590年代に、3.14159265358979323846…まで正しく計算した。bionic libcのmath.h
libc/include/math.h
https://android.googlesource.com/platform/bionic/+/refs/heads/master/libc/include/math.h
などでは、M_PIが、3.14159265368979323846で定義されている。この精度の近似値が歴史上初めて得られた。van Ceulenは、計算を進めて35桁目まで評価を行ったそう

また、1600年前後のヨーロッパでは、天文学以外に、航海術や測量術のような分野での三角法の利用も一般的になってきた。


17世紀後半には、ヨーロッパで様々な関数の冪級数展開が与えられた。John Wallisの1656年の著作Arithmetica Infinitorumには、x^nの積分や、項別積分の考え方が書かれていて、実質的に√(1-x^2)のべき級数展開も知っていたようだ。

人類に知られていた最古のべき級数は、1/(1+x)のものだろうけど、項別積分すると、log(1+x)のべき級数展開を得られる。これは、1668年に、Nicholas Mercatorが"Logarithmo-technia"で書いたとされている。1/xの積分が、対数であることは、メルカトル以前に知られていた。

※)メルカトル図法の"メルカトル"とは別人。メルカトル図法の名前は、Gerardus Mercator(1512~1594)という人に由来する。

John Napierは、1614年に対数表を公表して、1617年には、イングランドのHenry Briggsが常用対数を提案した。ケプラーが1627年に作成したルドルフ天文表にも、対数表が含まれるようだけど、これは、Napierと独立にJost Bürgiが対数の発見者と言われるので、その成果かもしれない。これらの時点では、自然対数は、まだ使われていない

同じ頃、ケーララ学派と同様に、ヨーロッパでも、x^nの積分が計算され、nが負や分数の時の結果も得られていたが、n=-1の場合が、未解決として残った。

1647年に、Grégoire de Saint-Vincentは、正数a,b,c,dに対して、現代の記号で書くと
\displaystyle \int_{a}^{b}\dfrac{dt}{t} = \displaystyle \int_{c}^{d} \dfrac{dt}{t} \Leftrightarrow b/a = d/c
を示したらしい。今では、積分の変数変換をするだけで、すぐ分かる。そして、1649年に、Saint-Vincentの生徒だったAlphonse Antonio de Sarasaが、
L(x)=\displaystyle \int_{1}^{x} \dfrac{dt}{t}
とすると、L(xy)=L(x)+L(y)となって、対数と同じ性質を持つことを認識したらしい。

当時は、1/xの積分によって自然対数が定義され、幾何級数に項別積分を適用することで、log(1+x)の級数展開を得たのだろう。このべき級数を得た人は、他にもいたかもしれないけど、現在では、メルカトル級数と呼ばれることがある。

一方、Newtonは、Wallisの結果に触発されて、一般二項級数から始めて、逆三角関数の級数展開に到達したと信じられている。そして、形式的に逆関数を計算して、三角関数のべき級数展開を得たようだ。Newtonは、1669年に"De analysi per aequationes numero terminorum infinitas"を書き、この手稿は当時の学者の間で回覧されたらしい。

De Analysi per aequationes numero terminorum infinitas
http://www.newtonproject.ox.ac.uk/catalogue/record/NATP00204

が、その内容っぽい。ラテン語だけど、それほど長くはない。Google翻訳で訳すと、それなりの英語になるけど、読むのが面倒なので、書かれている係数だけ雰囲気で見ると、1/(1+x)や√(1+x)の級数展開らしきものが前半にあり、1/(1+x^2)と、その積分なども級数の形で書かれている。後半の方には、arcsinやsinの級数展開らしきものも、書かれている。

べき級数の積分や逆を、形式的に計算すること自体は難しくないけど、Newtonが、これらの級数と、三角関数・逆三角関数の関係を、どのくらい理解していたのか、イマイチ分からない。

James Gregoryは、メルカトル級数の結果を見て、1/(1+x^2)の積分から、arctan(x)の級数展開を発見したとされ、現在ではグレゴリー級数と呼ばれているけど、この級数自体は、Newtonの手稿にも見られる。Newtonが、この級数が、arctan(x)に等しいことを理解してなくて、Gregoryが、それに気付いたということなら、グレゴリー級数という名称は妥当だと思われる。もし、Newtonがarctanとの関係に気付いていれば、円周率の"Leibnitzの公式"にも言及しそうなものだけど、Newtonの手稿には見られないから、気付いてなかったのかもしれない

この手稿の内容は、John Collinsを経由して、James Gregoryにも伝わったようだし、John Collins,Henry Oldenburgを通じて、Leibnitzにも伝わったとされる。

James Gregoryは、1668年に、通称"アルキメデスの漸化式(Archimedean Double Sequence)"と呼ばれる二重数列が収束することを証明したらしい。収束先がarctan(x)を使って書けることは分かっていただろうし、この二重数列が満たす漸化式を使って、arctan(x)のべき級数展開を見つけることも不可能ではなかったはずだけど、Gregoryは、そういう道は、辿らなかったようだ。

いずれにせよ、ヨーロッパでは、1670年前後に、三角関数や逆三角関数や対数関数のべき級数展開が知られるようになった。現代の標準的な微積分学のカリキュラムでは、微分→積分の順で習うけど、インドでもヨーロッパでも、微分法が発展する以前に、まず積分と無限級数の計算が先に発展したようである


【補足】メルカトル級数が知られる以前に、自然対数の数値計算に興味を持つ人がいたかどうかは分からないけど、常用対数表が存在してたわけだから、x=1以外のどこか一点で、自然対数の値を決めれば、底の変換によって、自然対数の計算を行うことはできたはず。自然対数の値を計算する方法として、
(1)数値積分
(2)交代調和級数の利用
(3)アルキメデスの漸化式
などが考えられる。

(1)数値積分は最も安直な方法で、1599年に、イギリスのEdward Wrightが、緯線距離を計算するために、正割関数の積分を、数値的に計算したという例がある。正割関数の積分が、対数とtanの合成関数で与えられることは、1668年にJames Gregoryが公表したようなので、Wrightの計算結果を流用したことはないだろうけど、数値積分の発想自体は存在したようである。実際に実行した人がいたかは分からない

(2)交代調和級数が、\log(2)であることは、1659年に、イタリアの数学者Pietro Mengoliが発見したらしい。1659年にGeometriae speciosae elementaという本を出版しているので、これに含まれるのかもしれないけど、400ページ以上あるので、中を探す気は起きない。Roger Godementの解析学の教科書には、Mengoliは、積分の長方形近似から得られる式
\log(2) = \displaystyle \lim_{n\to\infty} \sum_{k=1}^n \dfrac{1}{n+k}
と、容易に得られる等式
\displaystyle \sum_{k=1}^n \dfrac{1}{n+k} = 1 - \dfrac{1}{2} + \dfrac{1}{3} - \cdots + \dfrac{1}{2n-1} - \dfrac{1}{2n}
から、交代調和級数の値に至ったと書いてある。この初等的な議論は、1650年代のヨーロッパでも可能だっただろうし、また、Mengoliが、メルカトル級数を発見しなかったことも納得がいく。

交代調和級数を直接計算すると、収束が遅いけど、1668年にイギリスのWilliam Brounckerは
The Squaring of the hyperbola
https://royalsocietypublishing.org/doi/10.1098/rstl.1668.0009
で、交代調和級数の初等変形で得られる級数を3つ書いている。Brounckerの細かい議論までは見てないけど、級数と収束値は
\log(2) = \dfrac{1}{1 \times 2} + \dfrac{1}{3 \times 4} + \dfrac{1}{5 \times 6} + \dfrac{1}{7 \times 8} + \cdots
1-\log(2) = \dfrac{1}{2 \times 3} + \dfrac{1}{4 \times 5} + \dfrac{1}{6 \times 7} + \cdots
\dfrac{3}{4} - \log(2) = \dfrac{1}{2 \times 3 \times 4} + \dfrac{1}{4 \times 5 \times 6} + \dfrac{1}{6 \times 7 \times 8} + \dfrac{1}{8 \times 9 \times 10} + \cdots
となる。最後の級数は、比較的少ない計算量で、それなりの評価を与える。

William Brounckerは、Brounckerの連分数展開で知られる人でもあり、Fermatが出したPell方程式の整数解を求める問題を解いた人でもあるらしい(Eulerが誤解しなければ、Pell方程式は、Brouncker方程式と命名されたはず)

余談として、Ramanujanのノート(Chapter IIの冒頭)
cf)Ramanujan's Notebooks
https://www.imsc.res.in/~rao/ramanujan/notebookindex.htm
では、同様に、積分の長方形近似の式(Notebook Iを見ると、おそらく、積分から、この式を得たのだろう痕跡がある)があって、類似の等式
2 \log_{e}(2) = 1 + \dfrac{2}{2^3-2} + \dfrac{2}{4^3-4} + \dfrac{2}{6^3-6} + \dfrac{2}{8^3-8} + \cdots
を導いている。この続きには、同じような公式が、いくつか記載されている(Brounckerの級数は載ってない)。Ramanujanも、最初は、簡単なことから始めたということが分かる。

Ramanujanのノートには、積分
\displaystyle \int \dfrac{x^m}{1+x^n} dx
の計算も見られる(NoteBook Iでは、Chapter Xにある。NoteBook IIでは、Chapter VIIIのN13や14)。これは、対数関数やarctanを含むとはいえ、有理関数の積分だから、今となっては別に面白いものではない(n,mを固定すれば、Mathematicaでも計算できる)けど、Gaussの日記でも触れられている(Entry54)ので、賢い人たちも、色々な一般化を試行錯誤したらしいことが窺える(Gaussは、単に、Eulerの著作で、この積分を見つけたのかもしれない)

(3)17世紀でも、自然対数が、"アルキメデスの漸化式"で計算できることに気付ける可能性はあったと思うけど、多分、誰もやってないっぽい。これについて、1972年に、An Algorithm for Computing Logarithms and Arctangentsという論文が書かれている(調和平均の代わりに算術平均を使ってるけど、同じこと)。17世紀だと一般項が書けなくて、(M(a,b)で、初期値(a,b)に対するアルキメデスの漸化式の収束値を表すとする時)、漸化式から導ける関係式
M(1+x,2\sqrt{x}) = \dfrac{1+\sqrt{x}}{2}M(1+\sqrt{x},2x^{1/4})
のみだと、収束先を定数倍を除いて決められず、"x=1以外に、最低でも、もう一点の値を決めれば..."という問題に戻ってしまう気もする。


ヨーロッパ→東アジア

中国では、イエズス会の宣教師らによって、1631〜34年頃に、『崇禎暦書』が編纂され、これにも、割円八線表という名前で、三角関数表が含まれていたらしい(sin,cos,tan以外に、1/sin,1/cos,cot,versine,coversineの合計8つの三角関数があったことが、八線表という名前の由来のよう)。


李氏朝鮮は、15世紀に、独自の暦書「七政算内編」、「七政算外編」を作ったとされる。前者は、授時暦を研究した成果、後者は、回回暦を研究した成果で、清を宗主国としていた時は、独自の暦と清の暦(時憲暦)を併用したらしい。

李氏朝鮮には、中国で散逸していた、元代の算術書『算学啓蒙』(朱世傑、1299年)が教科書として使われて残っていた。この本には、天元術と呼ばれる初等代数が含まれ、初期の和算家が受容・発展させたとされる。秀吉が、李氏朝鮮を侵略した時に、技術者も連行したらしいから、初期の和算家が、彼らから、数学を学んだことはありそうに思うけど、そういう話は聞かない。

医者の岡野井玄貞は、1643年の朝鮮通信使で来日した朴安期(容螺山)に暦学に関する問答を行ったと伝えられている。岡野井玄貞は、日本で最初に作られた暦(貞享暦)の作成者である渋川春海が暦学を学んだ一人でもある

李氏朝鮮でも中国の影響から、ヨーロッパの数学や科学の流入はあったようである。1602年に北京でマテオ・リッチが刊行した『坤輿万国全図』が1603年にもたらされ、その後も、機会あるごとに、漢訳西学書が持ち込まれたと考えられている。また、1631年に、鄭斗源が北京から帰国する折に、イエズス会宣教師ジョアン・ロドリゲス(彼は、1577年に日本にやってきて、1610年に家康に追放された後、1612年からは拠点を中国に移して活動を続けた。ロドリゲスの後任として家康の外交顧問になったのがイギリス人ウィリアム・アダムス)から、漢訳西学書や西洋の文物を贈与されたことが知られる。

とはいえ、李氏朝鮮は、ヨーロッパに対して、日本よりも厳格な鎖国政策を採用したので、19世紀より前には、宣教師の入国が許可されることもなかった。ヨーロッパの書物を直接輸入して自国で翻訳することもなかったようなので、ヨーロッパの知識は、中国の漢訳西学書を通じて得られるものに限定されていたようである。

cf)"朝鮮数学史"という本には、朝鮮内でのヨーロッパ数学の状況について、ある程度記述されていそうである(未読)
http://www.utp.or.jp/book/b306128.html



江戸時代前半の日本では、鎖国と共に、ヨーロッパの書物は、中国で書かれたものも含めて、全面的に輸入が禁止されていたので、日本には、1723年に清で刊行された『曆算全書』が、1726年に輸入された時に、三角法が伝わったとされている。

それ以前でも、三角関数について、オランダ人から学ぶ機会はあったかもしれない

紅毛流として伝来した測量術について(I)
https://repository.kulib.kyoto-u.ac.jp/dspace/handle/2433/172777

紅毛流として伝来した測量術について(II) : 三角関数表の伝来と二つの経路
https://repository.kulib.kyoto-u.ac.jp/dspace/handle/2433/232876

また、江戸時代初期には、イエズス会士カルロ・スピノラやウィリアム・アダムスのような人が滞在していて、数学や天文学を教えたと伝えられているから、その時にも、ヨーロッパ数学伝達の機会は存在した。


とはいえ、17世紀の日本に三角関数表が存在していたという物証はないっぽい。成立年不明の『算暦雑考』という本は、内容などから、建部賢弘(1664〜1739)の著作と推測されていて、日本最初の三角関数表を含むとされている。この本は、18世紀に書かれたものだろうけど、和算でも、17世紀には、正多角形の周長から円周率を求めようという計算は沢山なされていたので、三角関数表を作ろうと思えば、計算自体は容易だっただろう

建部賢弘の弟子である中根元圭(1662～1733年、弟子だけど年上)は、『曆算全書』が輸入された後、ヨーロッパ流の三角法の解説書として、『八線表算法解義』を書いた。成立年は1727年頃とされている。『算暦雑考』も『八線表算法解義』も成立年不明なので、どっちが先か分からない

無限級数は、18世紀前半に、何人かの和算家が使うようになった。何らかの無限級数について言及した初期の和算書は、以下のようなものがある

『綴術算経』(1722,建部賢弘):arcsin(x)^2の級数展開
『宅間流円理』(1722,鎌田俊清):sin(x),arcsin(x)の級数展開
『方円算経』(1739):arcsin(x)の級数展開
『算法綴術草』(1740):1/(1-x),√(1-x)の級数展開

arcsin(x)^2のべき級数は、1737年にEulerが証明したとされている。建部賢弘は、証明や成立理由を知っていたわけでなく、数値計算の結果から予想しただけらしい。

他の無限級数については、独自のものという可能性もあるけど、1701年に北京入りしたフランス人宣教師Pierre Jartoux(1669〜1720)が中国に、いくつかのべき級数を伝えたとされ、それが日本にも伝わった可能性がある。Pierre Jartouxは、Leibnizと文通していたらしいから、高い学術能力を持った人だったようである。

天体観測については、吉宗の指示のもと、1744年に佐久間天文台が設置された

Pierre Jartouxの後、清代の中国では、明安図(1692-1763,Ming Antu)や項明達(1789-1850,Xiang Mingda)のような人たちが、無限級数の研究を継続していたらしい。項明達は、楕円の周長と長径の比を、離心率の無限級数で書けることを発見していたようだ。同様の結果は、ヨーロッパでは、1742年に、マクローリンが公表したとされている。

補足:楕円積分研究の動機

中国は、楕円の周長計算によって、微妙に、楕円積分に踏み込んでいたようだけど、一方、18世紀ヨーロッパで、楕円積分の研究が盛り上がった理由は、平面弾性曲線にあったっぽい。1742年のマクローリンの本には"The construction of the elastic curve, and of other Figures, by the rectification of the conic sections"というタイトルの章があり、楕円積分と平面弾性曲線の関連に触れているようだ

The elastica: a mathematical history
https://www2.eecs.berkeley.edu/Pubs/TechRpts/2008/EECS-2008-103.html

によれば、弧長を独立変数にして弾性曲線の微分方程式を書き、振り子の運動方程式と等価になる(つまり、平面弾性曲線が可積分系で記述される)ことに気付いた人は、Kirchhoffらしい(1859)。

このことは、Eulerが知っていたと書いている本もあり、出典は、1744年のEulerの本
Methodus inveniendi lineas curvas maximi minimive proprietate gaudentes, sive solutio problematis isoperimetrici lattissimo sensu accepti
https://archive.org/details/methodusinvenie00eule
だそうだけど、300ページ以上あるので、確認する気にはならない。

考えてみると、18世紀には、Euler topやLagrange topなども発見されたのだろうし、これらの解を記述しようと思って、楕円関数に辿り着いた人がいないのは不思議に思える。

cf)弾性曲線と可積分系の関係については、以下の解説が詳しい。
Lectures on Elastic Curves and Rods
https://doi.org/10.1063/1.2918095

おまけ:惑星運動と調和振動子

天動説であれ、地動説であれ、昔の人が最初に考えたモデルは、等速円運動
(x(t) , y(t)) = (R \cos(\omega t) , R \sin(\omega t))
だったらしい。等速円運動モデルが観測と合わないことは、割とすぐ認識されて、色々と複雑なモデルが作られることになった。等速円運動モデルは、今から見ると二次元調和振動子の特殊解になっている。

Keplerが楕円運動を提案した時、ガリレイ(やデカルト?)の反対があったらしいので、円運動への拘りは天動説よりも強かったのだろう。その後、NewtonやJakob Hermannの研究によって、惑星運動と調和振動子は、特に関係がなくなった

1906年に、Levi-Civitaは、三体問題の正則化に関する論文で、新しい時間変数と空間変数を導入した
Sur la résolution qualitative du problème restreint des trois corps
https://projecteuclid.org/euclid.acta/1485887161

Levi-Civitaの目的は三体問題だったので、特に明記されてないけど、この変数を使うと、Kepler系は調和振動子に帰着する。解析力学で、正準変換を使って問題を解く時、時間変数は据え置きにされるけど、時間変数も取り替えたほうがいいという教訓を与えてくれる例でもある

古典Kepler系の解析解
https://vertexoperator.github.io/2016/12/01/kepler2d_classical.html

こうして、惑星運動と調和振動子の間に、再び、関連が生まれた

表現論と信号処理

SU(1,1)あるいは、SL(2,R)の既約ユニタリ表現には、limit of discrete seriesと呼ばれるクラスのものが、2つある(一方は、他方の反傾表現になっている)。limit of discrete seriesは、直訳すると、"離散系列の極限"だけど、極限離散系列とかいう言葉は、耳慣れない気がするので、そのまま、limit of discrete seriesと書くことにする(検索すると、極限離散系列表現でも、何件か引っかかる)。

1947年に、Bargmannが、SL(2,R)の既約ユニタリ表現を分類した時、とある可約な連続主系列表現を直和分解することで、2つのlimit discrete seriesを構成したらしい。一旦、構成されてしまうと、特に複雑なものでもないので、何気なく、見過ごしてしまいそうだけど、Bargmannの構成は、古典的なPaley-Wienerの定理を、表現論的に捉えたものだとも解釈できる(多分、Bargmannは、別に、そんな風には理解してなかったんじゃないかと思うけど)。

Paley-Wienerの定理は、Hardy spaceのFourier変換による像が、[0,∞)上のL^2関数に等しいと書かれることもあるけど、L^2(R)を、(-∞,0]上のL^2関数と[0,∞)上のL^2関数の空間に直和分解できると見ることもできる。この2つの直和成分上に、2つのlimit of discrete seriesを実現できる。

実信号をFourier変換して、正の周波数成分のみを逆Fourier変換したものを、解析信号と呼ぶ(Gabor,1946)。これは、L^2(0,∞)を逆Fourier変換で戻しているので、解析信号は、Hardy spaceの元になる。当然、負の周波数成分のみを逆Fourier変換することも可能で、実数上の二乗可積分関数空間が、解析信号のなすHardy spaceと"反解析信号"のなす空間と、2つの空間に直和分解する。

また、実信号に対して、この信号を実部とする解析信号の虚部を与える変換は、ヒルベルト変換と呼ばれている。Hilbertは、Riemann-Hilbert問題の特殊ケースを解くために、この変換を導入したと、Wikipediaに書いてある。ヒルベルト変換は、物理では、Kramers-Kronigの関係式で現れる。


これらの定理や概念が発表された時期をまとめると、以下のようになる。

1926~27 Kramers-Kronigの関係式
1934 Paley-Wiener theorem
1946 解析信号(Gabor)
1947 SL(2,R)の既約ユニタリ表現の分類,特にlimit of discrete seriesの構成(Bargmann)

似たようなことが、異なる文脈で、何度も発見されて重要視されているので、多分、重要なんだろう

[0,∞)上のL^2関数空間は、Laguerre関数(Laguerre多項式に、exp(-x/2)をかけた関数)を、正規直交基底に持つことは、よく知られた事実である。Laguerre関数のFourier変換は、Wiener rational functionと呼ばれることがある。これを、更に、"Cayley変換"して、S^1上の関数と見ると、"exp(i n θ)"(nは非負整数)が得られる。指数関数/Wiener rational function/Laguerre functionという3種類の基底に対して、それぞれ、limit of discrete seriesの実現を与えることが出来る。円周上の関数としては、n<0に対しても、exp(i n θ)を考えたほうが自然であるけど、この部分に、丁度、もうひとつのlimit of discrete seriesを実現できる。そして、(-∞,0]上のL^2関数から、同様の操作を経ることで、得ることもできる

もう少し詳しい式は、以下に書いた

su(1,1)のlimit of discrete series
https://vertexoperator.github.io/2019/02/15/limit_of_discrete_series.html

su(1,1)のlimit of discrete seriesは、最高あるいは最低ウェイト表現で、この点については、su(1,1)のdiscrete seriesでも同様であるけども、二乗可積分表現でないため、連続ウェーブレット変換を定義することはできない(admissible vectorを持たない)。SL(2,R)の群作用は簡単に書けるけど、それが重要な理由は、よく分からない


ヒルベルト変換の工学的な応用としては、包絡線を書くのに使われる。物理や工学系のテキストで、殆ど周期的に時間変動する量を、瞬時値の一周期(あるいは適当な長さ)の時間平均として定義する、みたいなことが、よくある。この定義は、現実に観測される信号は、完全に周期的でないので、実用上は困る。ヒルベルト変換して、得られた解析信号の絶対値を定義とすれば、計算できる量となる。

偏角は位相を与えるわけだけど、例えば、音声信号(有声音)のピッチマーキング(周期点を発見すること)は、難しい問題で、完全な方法というのは、今も存在しない。ということで、音声信号にヒルベルト変換を施して、位相情報を取ると、どうなるか見てみた。

音声データは、

日本声優統計学会
http://voice-statistics.github.io/

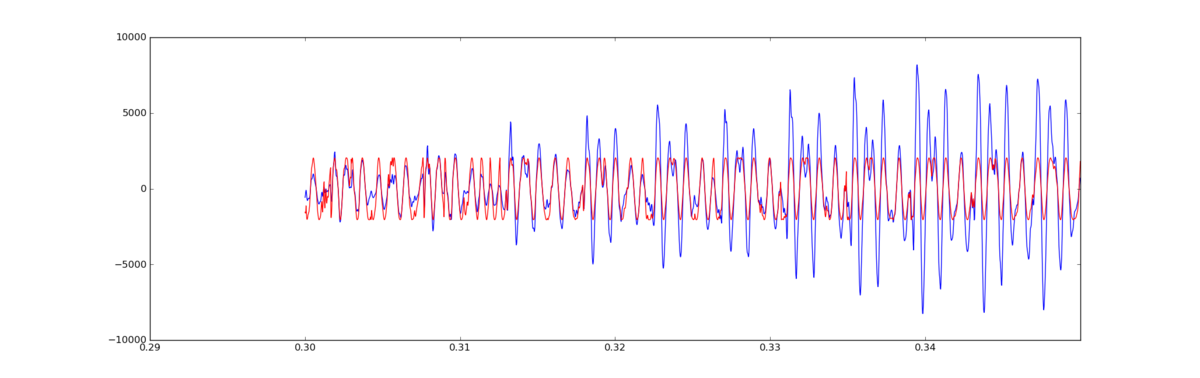
のtsuchiya_normal_100.wavを使用。冒頭の0.3〜0.35秒の区間("アーリー"の"あ"の音の一部)を抽出して、ヒルベルト変換を施し(scipyに含まれている)て、偏角を得、偏角のcosineを(見やすいように)定数倍して、音声信号と重ねた

f:id:m-a-o:20190401212516p:plain
ヒルベルト変換

青いのが、元音声の振幅で、赤いのが、ヒルベルト変換して得た位相(のcosine取って定数倍したもの)。まぁ、ピッチマーキングに使うことはできなそうだけど、ピークピッキングには使えそうな感じかもしれない


一般に、
(2x)^{\alpha/2} e^{-x} L_n^{(\alpha)}(2x)
の形の関数は、so(3,2)の極小表現のある実現(massless Klein-Gordon方程式の正エネルギー解を運動量空間で書いた時の基底)でも出てくる

so(3,2)の極小表現と波動方程式(書きかけ)
https://vertexoperator.github.io/2019/03/17/AdS4.html

多分、負エネルギー解の方も、同じような形の基底で書けるのだろう。数学的には、上の話の一般化というわけでもないのだけど、物理的には、関係が深そうな話ではある

単語の分散表現を使った教師なし単語翻訳

NLP

論文)Word Translation Without Parallel Data
https://arxiv.org/abs/1710.04087

実装)facebookresearch/MUSE
https://github.com/facebookresearch/MUSE


単語に実ベクトルを対応させるword embeddingsは、単語の分散表現の工学的な実現のように思われている。多分、本来は、distributed representation/分散表現は、脳内で外界の事象を符号化する方法として、局所表現と対をなす形で考えられた(NLP分野に限定されない)概念で、一方、word embeddingsは、単語をベクトル空間の点で表す工学的な手法を限定して指すと思うのだけど、日本語では、word embeddingsを指して、単に分散表現と呼ばれることが、しばしばあるっぽい。以下では、細かいことは気にせず、word embeddingsのことを、分散表現と呼ぶことにする。

2013年に公表されたword2vecでは、加法構成性が成立していて、意味や概念を獲得していると解釈できることで、話題になった(king-man+woman≒queenなどの結果が成立する)。尤も、類似度を内積で測る場合、x-yと類似度が高くなるには、xと類似度が高くて、yと類似度が低ければよいので、別段、大したことではないのかもしれないけれど。その後も、word2vecの改良版が、沢山出ていて、GloveやfacebookのfastTextは有名っぽい(word2vec論文のfirst authorだったMikolovは、fastText論文でも、last authorになっている)

cf)Word Embeddingモデル再訪
http://www.orsj.or.jp/archive2/or62-11/or62_11_717.pdf


加法構成性が成立する分散表現が、異なる言語間で、どれくらい似ているかは、早い段階から調べられていて、機械翻訳への応用が想定されていたらしい(word2vecの開発者Mikolovは、2013年に、arXiv:1309.416のような論文を出している)

加法構成性のある分散表現で成立する、単語間の線形関係式は、言語に依存せず成立して欲しい。加法構成性を保つという条件は、写像fに関する方程式f(x+y)=f(x)+f(y)の形で書け、これが、任意の点x,yで成り立つというのは、コーシーの関数方程式の高次元版になっている。数学的なことに突っ込んでもしょうがないけど、病的な解を除けば、線形写像のみが、この方程式の解となる。

cf)Cauchy's functional equation for Rn
https://math.stackexchange.com/questions/186350/cauchys-functional-equation-for-mathbb-rn

また、分散表現では、単語の類似度を内積で測るので、よい分散表現間のマッピングでは、内積が保存されていてほしい。従って、十分によい分散表現の間では、内積を保つ線形変換=直交変換の中に、単語翻訳を近似する写像があると期待される(分散表現で、単語ベクトルの長さは、特に規格化されていないので、個別の単語ベクトルを定数倍しても、類似度は変わらないけど、次元数が単語数より小さい時は、特定の方向をスケールする自由度は、あんまり残らなそうに、直感的には思う)


まぁ、もう実装があるので、とりあえず、冒頭のMUSEを使ってみる。fastTextの開発グループによるものっぽいので、データは、fastTextで作成したものを想定しているらしい。自分でデータを用意してもいいけど、以下に、多くの言語に対するデータが公開されている
Wiki word vectors
https://fasttext.cc/docs/en/pretrained-vectors.html

Word vectors for 157 languages
https://fasttext.cc/docs/en/crawl-vectors.html


一応、気付いたことなど。

・Faissは、Windowsには対応してない(README.mdには、recommendedって書いてあるので、MUSEを動かすには必須ではない?)

・そこそこ、メモリが必要かもしれない。計算中のメモリを減らすには、--max_vocabを200000より小さい値に設定すると有効(計算も速く終わる。但し、fastTextバイナリファイルを使うと、全部読み込むんでしまうのでダメっぽい)。教師なしの場合は、max_vocabが75000以下の場合、--dis_most_frequentをそれより小さくしてやらないといけないっぽい(多分)

・教師あり/教師なし共に、最後のtrainer.exportで辞書を出力するっぽいけど、一旦、全データを読み込むっぽいので、メモリ8GBで足りない場合もあるよう。wiki.en.vecは単語数が250万以上あるせいかもしれない。但し、必要なのは、ベクトル空間の間の直交写像Wで、dumped/debug/(ランダム文字列)/best_mapping.pthに出力される(デフォルトでは、300x300の行列なので、大したデータ量ではない)から、trainer.exportはコメントアウトしてもOK(後から、自分で、個々の単語ベクトルに直交写像Wを適用した結果を計算すればいい。normalize_embeddingsを指定した場合は、それに相当する計算も自分でやる必要があるが、デフォルトではOFF)

・src/evaluation/evaluator.pyの"self.word_translation(to_log)"で、Ground-truth bilingual dictionariesを見にいくっぽい。README.mdに、沢山のペアについて、リンクを貼ってくれているけど、リストにない場合は、どうしようもない。教師なし学習の場合、この処理は不要ぽいので、コメントアウトすればいい(例えば、日本語単語ベクトルを、中国語単語ベクトル空間に埋め込みたいという時は、データが用意されてない)

・README.mdの例にあるen vs esのケースを、CPUのみで計算した場合、max_vocabを50000にして、教師なしで半日弱で終わった。教師ありは、もっと早い。速度的には、まぁ悪くない


【テスト1】実際に、README.mdにある、英語->スペイン語を計算してみる。以下のようなコマンドで計算した

python supervised.py --cuda False --src_lang en --tgt_lang es --src_emb data/wiki.en.vec --tgt_emb data/wiki.es.vec --n_refinement 5 --dico_train default 

python unsupervised.py --cuda False --src_lang en --tgt_lang es --src_emb data/wiki.en.vec --tgt_emb data/wiki.es.vec --n_refinement 5

README.mdを見ると、11万強の類似単語対が書かれたデータ(en-es.txt)へのリンクが貼ってあるので、教師なしで学習したWで変換した単語ベクトルを使って、英単語とスペイン語単語の類似度を測る。

生のwiki.en.vecやwiki.es.vecは、単語数が多すぎて、gensimで読むと、遅い(メモリも使う)ので、検証用に使った辞書は、適当に、4万〜6万単語で、足切りした(別に、gensimで読む必要はないけど)。単語ベクトルが得られた場合は、そこそこの類似度になっていた。計測結果は、以下の通りで、教師データの有無で差が殆どない

教師なしの場合:類似度の中央値0.652,平均値0.628
教師ありの場合:類似度の中央値0.652,平均値0.628

計測に使ったコードは、以下のようなもの(以下は、教師なしの場合の類似度の中央値と平均値を測定する例)

import gensim 
import torch
import numpy as np

src_model = gensim.models.KeyedVectors.load_word2vec_format("data/wiki.en.40k.vec")
tgt_model = gensim.models.KeyedVectors.load_word2vec_format("data/wiki.es.60k.vec")
W = torch.load("en_es_unsupervised_mapping.pth")
similarities = []
##-- https://dl.fbaipublicfiles.com/arrival/dictionaries/en-es.txt
for n,line in enumerate(open("data/crosslingual/dictionaries/en-es.txt")):
  src,tgt = line.strip().split()
  try:
     v0 = src_model[src]
     v = np.dot(W, v0)
     w = tgt_model[tgt]
     sim = np.dot(v,w)/np.sqrt(np.dot(v,v)*np.dot(w,w))
     similarities.append( sim )
  except:
     pass


similarities.sort()
print(similarities[len(similarities)//2] , sum(similarities)/len(similarities))


平均値と中央値が、ほぼ同一なので、少し違う手段で、直交行列を比較する。同一の単語ベクトルを、それぞれの直交写像で変換した結果が、最も"離れる"のは、いつかというのを見ればいいだろうと思われる。ここでの"離れる"の意味は、Euclid距離ではなく、コサイン類似度を意味する。従って、(Wx , W'x)/(x,x)が最小になるようなベクトルxを発見すればいい。=(Wx,W'x)/(x,x) = (W'^{T}Wx,x)/(x,x)であるから、W'^{T}Wの固有値を見ればよさそうに思える。実際には、固有値は、殆ど複素数になるけど、単語ベクトルは、実ベクトルだと考えられているので、固有ベクトルが、欲しいxになるというわけではない。が、理想的には、固有値は全部+1なので、そこから離れている固有値が多いと、問題がある(ワーストケースでは、-1が固有値として出てくる)

実際に

W = torch.load("en_es_unsupervised_mapping.pth")
W2 = torch.load("en_es_supervised_mapping.pth")
print( np.linalg.eig(np.dot(W2.T,W))[0] )

とかやると、固有値-1が、ひとつ存在するけど、大部分の固有値は、1に近いので、それほど悪くない。流石に、例として記載されてるだけあって、悪くない結果のように見える



【テスト2】異なるコーパスで学習した、同一言語間のマッピングを見る。具体的には、Common Crawlで学習したデータと、Wikipediaから学習したデータを使った

教師ありの実験をするために、en-es.0-5000.txtに含まれる英単語から、en-en.0-5000.txtを作った(対応する単語は、同一単語を指定)

結果、教師ありの場合、類似度中央値:0.728 , 類似度平均値:0.702を得た。

CommonCrawlで学習したベクトルを変換して、Wikipediaで学習したデータで最も類似度の高い単語が同一になる割合は、93%だった。コーパスに依存しない情報を、それなりに抽出出来ているらしい。

教師なしでやると、何故か、類似度中央値:0.086,類似度平均値:0.087で、計算に失敗しているらしかった。理由は不明


【テスト3】CommonCrawlコーパスから学習した、英語→スペイン語のマッピングを見てみる
python supervised.py --cuda False --src_lang en --tgt_lang es --src_emb data/cc.en.300.vec --tgt_emb data/cc.es.300.vec --n_refinement 5 --max_vocab 100000

python unsupervised.py --cuda False --src_lang en --tgt_lang es --src_emb data/cc.en.300.vec --tgt_emb data/cc.es.300.vec --n_refinement 5

教師あり学習の場合、類似度中央値:0.591,類似度平均値:0.574
教師なし学習の場合、類似度中央値:0.562,類似度平均値:0.549

Wikipediaコーパスの時より、少し下がっているものの、それほど悪くはない数値


【テスト4】テスト1と同様の計測を、英語→日本語でやってみた。

データは、Wikipediaから作ったらしいwiki.en.vecとwiki.ja.vecを使用した場合、
教師ありの場合:類似度の平均値:0.429 , 中央値:0.430
教師なしの場合:類似度の平均値:0.252, 中央値:0.240

単語対データen-ja.txtとen-es.txtは同じものではないので、単純に比較するわけにはいかないけれども、英語→スペイン語に比べると、やや低い値になっている。それ以外に、理由がよくわからないこととして、教師なしと教師ありの場合の差が大きくなっている

教師なしの方は、数値以上に悪い。単語対データの英単語を、日本語単語ベクトル空間にマッピングして、最も類似度の高い単語ベスト3に、対になる単語が含まれている割合を、教師ありと教師なしで比較したところ、教師ありの方は、12%だったが、教師なしの方は、一つもなかった。これは、何も学習できていないといって差し支えない結果である。引っかかる単語の大部分が、japanese_national_route_sign_のような単語ですらないゴミ。教師ありの方も、アルファベットで構成される単語と近くなる傾向が見られ、英語のpearlやclassに近い単語として、日本語側でも、pearlやclassが出てくる(ある意味、間違ってはいないが...)

アルファベットのみの単語を除去してマッピングしても、うまくいかなかったので、単語ベクトルの作り方が悪いのかもしれない。wiki.ja.vecには、japanese_national_route_signだの「アメリカ合衆国国勢調査局に拠れば」だの、単語でないものも含まれているし

cc.en.vec->cc.ja.vecだと
教師ありの場合:類似度の平均値:0.494 , 類似度の中央値:0.510
教師なしの場合:類似度の平均値:0.108 , 類似度の中央値:0.105
で、教師なしでは、うまくいかない。

教師ありの方は、そこそこ。類似単語トップ3に、対になる単語が入っている割合は、64%。トップ3に入ってないものの中には、june->8月、april->5月みたいな形で惜しい物、history->歴史(en-ja.txtには、履歴、由緒、沿革などがある)やhigh->高い(en-ja.txtには、ハイ)のように正解であるものも含まれる。

他に、aspirin->錠剤やfructose->糖分みたいなspecificityが高すぎて特定できてないものなどもあるけど、人間でも、アスピリンを「何か薬だよね」とか、フルクトースを、「なんか糖だよね」とかくらいしか理解してない人がいそうなことを思うと、許容範囲内の結果になってる。言語の違いにも関わらず、良好な結果を与えている

日本語に関しては、wiki.ja.vecには、問題があり、cc.ja.vecの方が、いいっぽい



【テスト5】Gloveで学習した単語ベクトルを使って、英語→英語を試してみる

GloVe: Global Vectors for Word Representation
https://nlp.stanford.edu/projects/glove/
に、異なるコーパスから学習したらしいデータが、いくつか公開されている。Wikipediaから作成されたらしいglove.6B.300d.txtと、Common Crawlから作ったらしいglove.42B.300d.txtを使って、今までと同様の計算をやる。これらのファイルは、fastTextと微妙にフォーマットが違っていて、ヘッダに、単語数と単語ベクトルの次元を追加する必要がある

教師ありの場合:類似度の中央値:0.61, 平均値:0.60, 最も類似度の高い単語が同一である割合:86.2%
教師なしの場合:類似度の中央値:0.62, 平均値:0.60, 最も類似度の高い単語が同一である割合:86.3%

Gloveで作ったデータでも、それなりの結果を得られた。この結果を、テスト2と比較すると、fastTextの方が、よい結果を与えるようにも見える。


異なるコーパスで学習した作った分散表現間でも、類似度が0.6〜0.7にしかならないのは、もうちょっと何とかなってほしい


【おまけ】
ついでに、ヴォイニッチ手稿に、この方法を適用すると、どうなるか試したけど、全ての単語が、","や"a","the","I"などの出現頻度が高い単語との類似度が高くなるように、直交写像Wが学習されてしまい、全然ダメだった(ヴォイニッチ手稿の分散表現は、fasttextで作った)。類似度は、殆どの場合、0.9以上あるので、Wの学習そのものが失敗してるわけではなく、むしろ、最適化を見つけてはいると言える。

この結果だけだと、ヴォイニッチ手稿の単語ベクトルの分布が、偏ってるのか、単語数が少ない(約1000単語)せいで、こうなってるのか分からないけど、聖書一冊(新約+旧約、約5400単語)でやっても、うまくいかなかったので、単語数が少ない時は、もう少し工夫がいるっぽい。そもそも、300次元はでかすぎるのかもしれないという可能性もあるけど、本一冊程度から学習できる程度では、単語ベクトルの点群がなす分布形状全体を網羅しないという方がありそうではある。


ヴォイニッチ手稿を選んだ理由は、思い入れがあるわけではなく、他の未解読文字でもよかったけど
・電子化されたテキストがあること
・分かち書きされた言語で書かれてること
という条件で扱いやすそうだったので、ヴォイニッチ手稿を使った。

ヴォイニッチ手稿の画像データは、以下で閲覧できる。
The Voynich Manuscript
https://archive.org/details/TheVoynichManuscript

ちょっと見れば分かる通り、素人目には判読しがたい。画像から(普通、手作業で?)テキストデータに変換することを、transcriptionと読ぶらしい。transcriptionには、行った人によって、複数のバージョンが存在し、統一的な見解というのは、ないようである。

以下の2つのページに、異なるtranscriptionが存在し、似てはいるものの、同一ではない。musyoku/voynich-transcriptionは、大体、20万文字ちょっとになるよう。
musyoku/voynich-transcription
https://github.com/musyoku/voynich-transcription

Voynich Manuscript-transcription
http://www.voynich.com/pages/index.htm

他に、以下のページでも、複数のtranscriptionが入手できる
Reeds/Landini's interlinear file in EVA, version 1.6e6
http://www.ic.unicamp.br/~stolfi/voynich/98-12-28-interln16e6/

未知の文字のOCRは、不可能でないにしても、そこで、間違いが混在する可能性が高いので、先人がテキストに起こしてくれていることが望ましい。あと、個々の文字の判読は難しいけど、なんか、分かち書きされてることは分かる。日本語や中国語のように、分かち書きされてない言語だと、分かち書きするとこから始めないといけない。無教師で分かち書きも、現在の技術で出来ないこともないかもしれないけど

使用した聖書のデータは、Project Gutenbergから引っ張ってきた英語版。

The King James Version of the Bible
http://www.gutenberg.org/ebooks/10

非外科的な豊胸手法

ある時、女性ホルモン(エストロゲン)の分泌量の推移を眺めていたら、ピークが10代ではなく20代にあることに気付いた。が、胸部サイズの成長は、むしろ10代に起こるだろうと思われるので、そう考えると、何らかの成長ホルモンの方が、支配的な影響を及ぼしているのかもしれない。当然、成長ホルモンは、男性でも分泌されるから、女性ホルモンも一定量は必要なのだろうけど、20代女性でも、成長ホルモンを補ってやれば、胸部の成長が起きるかもしれない、と予想した。

成長ホルモンと聞いて、思いつくのは、hGH(ヒト成長ホルモン)であるけども、他の成長因子が重要である可能性もある。少し文献を調べると、IGF-1と胸部サイズの相関が最も高いらしいことが分かったので、被験者(当時、20代半ば。標準的な体型)を探して、テストしてもらった(方法を説明して、定期的にお金を渡した。美味しいものを食べるのに使われたりしてないことは確認した)

その時に、説明した内容がこれ↓

非外科的な豊胸手法
https://gist.github.com/vertexoperator/e4839407ae85d45f26189b378cc5edeb

協力してもらった被験者の方は、Aカップ未満から、概ね、一年に一サイズくらい成長したらしい。当初は、一年くらいの予定だったのだけど、結局、5年強も実験を継続した。年齢的なことと、お金が尽きたので、実験は終了。エストロゲン分泌量は、40歳くらいでも、10代半ばくらいの水準はあるようなので、30代でも効果はあるかもしれない。

残念ながら、被験者は、一人しか確保できなかったので、全然実証には、なってない。5年で、500万円くらい消費したので、複数の被験者を集めたりすることは、金銭的に厳しい。

IGF-1で検索すると、スプレーとか、そういうのが、沢山出てくるけど、99.999%効果はない。IGF-1が含まれているかどうかも怪しいし、含まれていても、液体に溶かした状態で置いておけば、急速に分解していく

外科的な手法と比較すると、

・豊胸手術として一般的に想像されるのは、インプラントを皮下に注入する方法であるけども、外科的手法なので、暫くは、相当痛いらしい。こっちは、注射の痛みのみ
・豊胸手術の方が、安価かつ短期間に、大きな効果を得られる。こっちは、時間と金がかかる
・注射痕が残る可能性がある

という感じだろうか。Wikipediaには、「日本の厚生労働省は、その他いずれの乳房インプラントも薬事承認しておらず、安全性に関して保障していない」と書いてある。安全性が保証されない点は、同じようなものだろうか。こっちは、本当に効果があるかも怪しいので、不利だけど



これについては、個人的には、満足のいく結果になったので、これ以上は、追求しない。あとは、お金が回復したら、やろうかと思ってる人体実験の話。こちらは、自分自身で実験するつもりなので、気が楽

以前に、食物由来のmiRNAが体内に取り込まれている可能性が話題になった。
Exogenous plant MIR168a specifically targets mammalian LDLRAP1: evidence of cross-kingdom regulation by microRNA
http://www.nature.com/cr/journal/v22/n1/full/cr2011158a.html

これについては
Mining of public sequencing databases supports a non-dietary origin for putative foreign miRNAs: underestimated effects of contamination in NGS
https://www.ncbi.nlm.nih.gov/pubmed/24729469
などで否定的な見解が示されていて、また、その他のケースでも、miRNAは消化されてしまい、吸収されるまでに到達しないという結果がいくつか報告されている


では、腸内で細菌にsiRNAを産生させればどうかと考える。通常、殆どの菌や細菌は、経口投与しても消化されてしまい、腸まで生き延びることはできないものの、ある種の乳酸菌は、生きて腸まで届くと宣伝されている。乳酸菌は、様々な菌の総称なので、全ての乳酸菌が消化に耐えるわけではなないらしいが、消化に耐える乳酸菌を遺伝子組み換えによって、siRNAを産生させるようにすれば、腸内でどんどんsiRNAを生産し、それが吸収され、効果を発揮するかもしれない。実際には、siRNAが血中に取り込まれるとしても、それが細胞に取り込まれるかどうかは別問題であるけれども。


乳酸菌は至るところにいるので入手に問題はないけれど、問題は、一般家庭で遺伝子組み換えを行うことは、そんなに容易いことではないという点。DIYBIOという、非研究機関外の人々による生物実験を行うmovement界隈には、"glow-in-the-dark-yogurt"という、GFP遺伝子を導入された乳酸菌で作ったヨーグルトの伝説がある。これが、本当に行われた実験なのかよく分からないし、プロトコルなども公開されていないようなので、あんまり役立つ情報ではない。原理的には、siRNA発現部位と抗生物質耐性遺伝子を持ったリニアなDNAを導入して、相同組み換えを起こすのが、一番楽だとは思うのだけど、それでも課題はある

※)腸溶性カプセルに、細菌を詰めて飲めば、生きて腸まで届くのでは、という気もする。実際、ビフィズス菌のカプセルというものはあるらしい(が、信用できる商品なのかどうかまでは確認していない)。ローテクで済むのであれば、カプセルなしで済ませたいという気もするが、一方で、大腸菌などに、siRNA発現プラスミドを導入する方が、実験としては容易かもという気持ちもある(分子生物学実験をやったことのある人のほとんどは、大腸菌を扱った経験があるだろうし、それだけ色々と知見もあるということであるし)

乳酸菌以外の選択肢としては、納豆菌も候補になりうる。


最近、検索して、類似のことを考えていた研究者が居たのを発見した。
RNAi創薬を目指したRNAデリバリー技術の開発
https://kaken.nii.ac.jp/ja/grant/KAKENHI-PROJECT-20015032/
によれば、"現状ではshRNAのみを産生する乳酸菌株を作製し、マウスにおいてこの乳酸菌を投与することで特異的なRNAi効果が起こることを見いだした。今後CPP-RBPとshRNAの共発現系を内包する乳酸菌を作ることにより、このRNAi効果がより顕著になることを期待している。"とある。CPP-RBPというのは、siRNAの細胞内導入効率を高めるべく設計されたタンパク質らしいが、それがなくても、RNAi効果が確認できた(どれくらいの効果があったのかは論文読まないと分からないが)ということで、よいニュースではある。研究者たちは、癌治療の手法として、この方法を考えたらしいけど、私見だと、癌治療にRNAiを使うのはgood ideaとは思えない。その後、研究を断念したのか、どうなったのかは不明


どっちかというと、HIV治療とかの方が見込みがありそうな感じではある。
RNA interference approaches for treatment of HIV-1 infection
https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4445287/
HIV治療に使う(HIVを体内から根絶する)には、上のCPP-RBPのように、細胞内導入効率を高める工夫が必要かもしれないし、それを乗り越えても、"mutation escape"という課題があり、単一のsiRNAで根治というわけにはいかないと思うけど。ただ、HIV治療に使えるなら、原理的には、他のRNAウィルス(インフルエンザウィルス、ノロウィルス、エボラウィルスetc.)でも何かしら使えるかもしれない。

私自身は、特に困ってないので、病気の治療に興味はないから、適当に、自分の遺伝子発現を抑制できるか見たい。ターゲット遺伝子は何でもいいけれど、できれば発現を抑制して有益な効果をもたらす遺伝子がいい。現在、候補として、ミオスタチンを考えている。これは、ミオスタチン関連筋肥大で知られる遺伝子で、筋肉の成長を抑制する働きがあり、生まれつき欠損していたりする場合、筋肉が異常に成長するらしい。というわけで、可能性としては、「トレーニングしないでも食べるだけで、筋肉が成長していくヨーグルト」というものが作れるかもしれない。

研究室と違って、基本的な試薬も実験機器もないので、色々方法を考えないといけないし、差し当たって、お金がない

光の位相演算子

誰か、闇の位相演算子も定義してほしいと思ったけど、ダークソリトンとかあるし、頑張れば何とかならないのだろうか

本題。量子力学に於ける不確定性原理は、可換でない演算子の組があれば成立するものの、

(1)時間とエネルギーの不確定性関係に於いて、時間演算子は存在しないという批判
(2)光子数と位相の不確定性関係に於いて、位相演算子の定義に問題がある件
(3)相対論的量子力学に於いて、光子の位置演算子の定義ができないという問題

など、基本的であっても、演算子の定義自体が問題とされるケースも多い。

(1)の時間とエネルギーの不確定性関係は、1927年のHeisenbergの論文にも書かれているけど、Pauliによって批判されたらしい。Hamiltonianと正準交換関係を満たす時間演算子があれば、Hamiltonianが無限小時間並進演算子なのと同様、時間演算子は、"無限小エネルギーシフト"演算子となるけど、エネルギーは勝手にシフトすると、固有状態が存在しなかったりするので、不都合となる。時間演算子を使わず、時間とエネルギーの不確定性関係を導く議論も多々ある。ただ、位置と運動量の不確定性関係の場合、位置演算子と運動量演算子の同時固有状態が存在しないのと比べて、時間とエネルギーについては、そもそも同時固有状態という考え方が適用できない。形式的に同じような式が出ても、物理的意味が同じと言えるのか、よく分からない

(3)の問題の発端は、1949年のNewtonとWignerの以下の論文にある。
Localized States for Elementary Systems
https://journals.aps.org/rmp/abstract/10.1103/RevModPhys.21.400

この論文では、単一の相対論的自由粒子の位置演算子をどう定義するのかという問題に、部分的な解答を与えている。相対論的自由粒子なので、考える状態空間は、ポアンカレ代数の既約ユニタリ表現となる。massiveな場合は、ポアンカレ代数の生成元の(非可換)有理式で書かれる演算子が存在し、位置演算子となるとしている(現在では、Newton-Wigner演算子と呼ばれる)。masslessの場合は、これは、うまくいかないらしい

普通の量子力学では、状態空間を[L^2(\mathbb{R}^3)]に選んでるとか、あるいは、同じようなことだけど、CCR代数の表現空間に選んでいるという理由で、位置演算子の定義は、問題なくなっている。これはこれで、相空間T^{*}\mathbb{R}^3(上の関数環)を量子化したから〜といった正当化が与えられているけど、Newton-Wignerの問題設定とパラレルに考えると、非相対論的な自由粒子の状態空間は、ガリレイ代数の既約ユニタリ表現空間となる。この場合は、無限小Galilean boostの位置演算子の1/mが位置演算子を与えると思える(mは粒子の質量)。古典的には、これは、重心座標を表す保存量なので、一粒子系では、粒子の座標と思って、差し支えない。ガリレイ代数の場合でも、massless particleを考えられるけど、m=0では、位置演算子が作れないので、相対論的な場合と、問題は同根じゃないかと思う。

【補足】ガリレイ代数の場合でも、massless particleを考えられることの反映として、電磁気学の非相対論的極限などが存在する。研究の嚆矢は1960年代にあるようだけど、1973年以来、これは、Galilean electromagnetismという名前で知られている。面白いことに、非相対論的極限には、magnetic limitとelectric limitの二種類がある。以下の論文によれば、二種類ある理由は、斉次ガリレイ群(ガリレイ群から、並進を除いたもので、Lorentz群の非相対論版)のベクトル表現は、二つある(彼らの記号では、D(1,1,0),D(1,1,1))からと書いている。
Galilei invariant theories. I. Constructions of indecomposable finite-dimensional representations of the homogeneous Galilei group: directly and via contractions
https://arxiv.org/abs/math-ph/0604002
斉次ガリレイ群の4次元表現として、誰でも知ってるものは、Galilean boostによってx_i \mapsto x_i + v_i x_0(i=1,2,3)と変換するものがある(v_iは、パラメータで、x_0は時間変数に相当する)。これの行列表示を転置したものも、Lorentz群のベクトル表現の非相対論的極限で、得られるということらしい



(2)の問題は、波数や周波数が単一のモードであるような、量子光学的なモデルで考察される。状態空間は、光子の生成・消滅演算子を真空に繰り返し作用させて張られる空間で、数学的には、調和振動子の系と変わらない。粒子数演算子は問題なく定義できるけど、位相演算子の方は、謎がある。この問題に最初にアプローチしたのは、Diracだとされている。
The Quantum Theory of the Emission and Absorption of Radiation
https://royalsocietypublishing.org/doi/abs/10.1098/rspa.1927.0039

古典的には、実信号が、解析信号V(t)の実部となっている場合(例えば、電磁波を受信して得られた、生の電気信号があるというような場合、解析信号の計算は、原理的にはヒルベルト変換を使えば出来る) 、以下の極分解がある
V(t) = \sqrt{I(t)} \exp(i \phi(t))
I(t)が強度で、\phi(t)は位相。

量子論に於いては、消滅演算子のpolar decompositionが
\hat{a} = e^{-i \Phi} \sqrt{N} = \sqrt{N+1} e^{-i \Phi}
で定義される。Diracの論文の式(10)には、生成・消滅演算子のpolar decompositionが書かれている。Nは粒子数演算子で、単一モードで考えているので、光子数と全エネルギーは比例するから、強度演算子と呼ばれることもある。E=e^{-i \Phi}の部分は、現在、Susskind-Glogower演算子という名前で呼ばれているものと同じ。

Susskind–Glogower operator
https://en.wikipedia.org/wiki/Susskind%E2%80%93Glogower_operator

Susskind-Glogower演算子は、調和振動子の生成・消滅演算子の(非可換)多項式の形では書けないけど、状態空間の正規直交基底を、|0>,|1>,...とすれば
\sqrt{n} |n-1\rangle = a|n> = E \sqrt{N} |n \rangle = \sqrt{n} E|n \rangle
であるから、
E = |0\rangle\langle 1| + |1\rangle\langle2| + \cdots
とすればいい。こうすると、E\sqrt{N} = \sqrt{N+1}Eが消滅演算子と等しいことは容易に分かる。従って、消滅演算子の極分解自体は、ちゃんと存在する。測定可能量はエルミートであることが必要だけど、(E+E^{\dagger})/2,(E-E^{\dagger})/2iと分解すれば、エルミート演算子を得ることはできる。

単一モードで考えているので、量子化した電場は、規格化因子を除けば、
\hat{\mathbf{E}}(\mathbf{r},t) = i \omega \mathbf{e}(\hat{a} e^{i(\mathbf{k}\cdot\mathbf{r} - \omega t)} - \hat{a}^{\dagger}e^{-i(\mathbf{k}\cdot\mathbf{r} - \omega t)})
という形で書け(\mathbf{e},\omega,\mathbf{k}は偏光ベクトル、周波数、波数。偏光ベクトルは実であるとする)、コヒーレント状態に対する、量子化した電場の期待値は
\langle \alpha| \hat{\mathbf{E}}(\mathbf{r},t) | \alpha \rangle = -2 \omega \mathrm{Im}(\alpha e^{i(\mathbf{k}\cdot\mathbf{r} - \omega t)}) \mathbf{e} = -2 \omega |\alpha| \sin(\mathbf{k}\cdot\mathbf{r}-\omega t + \theta) \mathbf{e}
となる。\alpha = |\alpha| e^{i \theta}で、\thetaが欲しい位相になる。これは、絶対位相で、座標原点の取り方に依存した量だから、直接観測できる量ではないだろうし、理想的な位相演算子が存在しても、それ自体は、観測できない量になると思われる

コヒーレント状態に対する位相演算子の期待値は、\alpha/|\alpha|になるのが理想だけど、Susskind-Glogower演算子の期待値を計算すると、厳密に、このような量にはならない
\langle \alpha | E | \alpha \rangle = \alpha e^{-|\alpha|^2} \sum_{n=0}^{\infty}\frac{1}{\sqrt{n+1}} \frac{|\alpha|^{2n}}{n!}
である。まぁ、絶対値は1でないけど、位相成分は一致してるし、古典的な光学で利用される光では、光子数は非常に大きく(例えば、平均出力1mW、波長500nmのレーザー光は、毎秒10^15個オーダーの光子を放出している)、
e^{-x} \sum_{n=0}^{\infty}\frac{1}{\sqrt{n+1}} \frac{x^n}{n!} \approx \frac{1}{\sqrt{x}}
が、大きいxでは成立していそうなので、許容できるかもしれない(数値実験した範囲では、これは正しいようだけど、証明は知らない)

古典的な場合と異なり、EとNは可換でないから、同時固有状態は存在せず、位相と強度には、何らかの不確定性関係があることになる。簡単な計算で、[E,N]=Eであることが分かる。この交換関係は、円周上の北門・大貫代数と呼ばれるものと同じ。この関係式自体は、形式的には、sl(2)のChevalley基底([h,e]=2eや[h,f]=-2f)だったり、ax+b群のLie環の関係式だったりでも見ることができるけど、(仮想的な)"位相演算子"\Phiに対して、e^{-i \Phi}に相当する演算子を作りたいという発想なので、Eは、(適当な表現空間上で)ユニタリーであってほしい。これは、sl(2)やax+b群のとは、話が違う

形式的な計算では、
|\theta \rangle = \sum_{n=0}^{\infty} e^{i n \theta} |n \rangle
という状態に対して、
E|\theta \rangle = e^{i \theta} |\theta \rangle
が成立する。ただ、E|0\rangle = 0でもあるので、ユニタリーではない

ユニタリー性を破るのは、真空|0>の場合のみで、真空はα=0のコヒーレント状態であるから、素朴に考えると、位相はα/|α|=0/0で、不定となる。古典的にも、強度が0であれば、位相を定義することはできない。数学的には、極座標で、原点の表示が一意に決まらないことに対応する。プログラミングなら、なんか例外を投げたいとこではある。位相が不定になる唯一の状態を、固有値0の固有状態に持つのは、利点にも見えるけど、ユニタリー性を破る原因でもあるので、欠陥だと考える人もいる


Susskind-Glogower演算子は、粒子数シフト演算子になっている。これは、エネルギーや運動量が、時間や位置の無限小並進演算子なのと類似している。もし、光子数に下限がなければ、粒子数シフト演算子は、完璧な位相演算子を定義する。正規直交基底が、|0>,|±1>,|±2>,...ととれる場合、粒子数演算子の素直な類似は
N |n \rangle = n|n \rangle
であり、またSusskind-Glogower演算子の類似として
V |n+1 \rangle = |n \rangle
と取れる。NとVは、hermitian operatorとunitary operatorであり、形式的に
|\theta \rangle = \sum_{n=-\infty}^{\infty} e^{i n \theta} |n \rangle
とすると、これは、Vの"固有状態"となる(自身との内積が発散するから、数学的には、固有状態ではないけど)
V | \theta \rangle = e ~{i \theta} | \theta \rangle
そして、今度は、V^{\dagger}の固有状態でもある。また、NとVは、交換関係
[V,N]=V
を満たすので、円周上の北門・大貫代数の"ユニタリ表現"を与えている(Vがユニタリ演算子で、Nがエルミート演算子の時、ユニタリ表現と呼ぶのが適切。既に見た通り、単一の調和振動子の状態空間にも、北門・大貫代数の表現が定義できたが、"ユニタリ表現"にはなっていなかった)

円周上の北門・大貫代数のユニタリ表現から、2次元Euclid代数のユニタリ表現を作ることが出来る。(複素)2次元Euclid代数は、生成元D,X,Yと交換関係
[D,X]=Y,[D,Y]=-X,[X,Y]=0
で定義され、エルミート共役を取る操作(Lie環に内在的に定義されるCartan involutionは、ユニタリ表現上で、歪エルミート共役を取る操作になるので、そのマイナスのこと)で
D^{*}=-D , X^{*}=X , Y^{*}=Y
のように変換されるとすると、
D = i N , X =\frac{1}{2}(V + V^{\dagger}) , Y= \frac{1}{2i}(V - V^{\dagger})
によって、2次元Euclid代数のユニタリ表現が定まる。Vはエルミート演算子でないけど、XとYは、エルミート演算子になっている。

Vの実部Xと虚部Yは、Vのユニタリー性から可換でないといけない。調和振動子の空間で、生成消滅演算子も実部と虚部に分けることができ、初等的な量子力学では、位置演算子と運動量演算子に対応するので、可換ではない。量子光学では、位置と運動量ではなく、直交位相振幅とか呼ばれることが多い

円周の座標を\phiとして、|n>が円周上の関数e^{-i n \phi}であれば、
D \mapsto -\frac{d}{d \phi} , X \mapsto \cos \phi , Y \mapsto \sin \phi
としても同値な表現を得る。北門・大貫代数の定義式[V,N]=Vは、
[e^{i\phi} , i \frac{d}{d\phi}] = e^{i\phi}
と同じものと解釈できる。このような系は、円周上の量子力学と等価で、"位相演算子"Vが、円周上の位置演算子の役割を果たし、粒子数演算子は、円周上の運動量演算子に相当する。そういうわけで、円周上の北門・大貫代数は、CCR代数の変種であって、Susskind-Glogower演算子は、非常に惜しいことが分かる



光子の位相演算子としては、Pegg-Barnett位相演算子というのも、よく見かける。論文は、1989年に出ている

Phase properties of the quantized single-mode electromagnetic field
https://journals.aps.org/pra/abstract/10.1103/PhysRevA.39.1665

Pegg-Barnettの方法では、有限準位系に対して、(ユニタリーな)有限位相演算子を定義して、極限を取って、無限準位に移行するけど、数学的に正当化できるかは疑わしい



絶対位相は、位相演算子が定義できても、どうせ観測できないはずの量だから、位相差演算子が存在すればいいという考え方もありうる。

偏光状態の記述でよく使われる物理量に、Stokesパラメータがあり、測定装置なども販売されてるらしい。Stokesパラメータには、量子版のStokes演算子が存在して、偏光状態の記述に限らず、一般の2モード状態で定義できる。コヒーレント状態に対するStokes演算子の期待値を見ると、位相差に関する量を含んでいる。

(単一光子状態などでも使える)直交位相振幅の測定法として、バランス型ホモダイン測定という手法があるらしいけど、バランス型ホモダイン測定に於ける測定量は、2モードに於けるStokes演算子(の一つ)と見なせるようである。入射する光の一方が、コヒーレント状態にある光であれば、計算によって、直交位相振幅を測定できることが分かる(※)

※)参考文献:古澤明『量子光学の基礎』16〜17ページ。Stokes演算子とは書いてないけど、この本の中で、"バランス型ホモダイン測定の出力"だと書かれている式(1.64)は、Stokes演算子の一つになっている


Stokes演算子の期待値が位相差に関する情報を含んでいても、Stokes演算子自体は、位相差演算子ではない(丁度、単一モードでは、消滅演算子の固有状態がコヒーレント状態であるけど、消滅演算子は位相演算子そのものではないのと同様)から、2モードで位相差演算子を定義できるかというのは、自明な問題でもない。1993年に

Phase-difference operator
https://journals.aps.org/pra/abstract/10.1103/PhysRevA.48.4702

という論文が出ている。基本的には、位相差演算子が満たしてほしい条件(2.5a)(2.5b)を提示し、この2つの条件を満たしつつ、ユニタリー性を備える演算子(今までと同様位相のexponentialを与える演算子なので、エルミートではなく、ユニタリーであることを要求する)は存在しないので、どうしようという話。条件(2.5a)は、位相差演算子は、総粒子数演算子と可換という条件で、条件(2.5b)は、位相差演算子と相対粒子数演算子(の1/2)が、円周上の北門・大貫代数をなすという条件。

論文の条件(2.5a)(2.5b)が、自然であることは、例えば、以下のように考えれば分かると思う。仮に、2つの独立な北門・大貫代数(Nはエルミートと仮定する)
[E_1,N_1]=E_1 , [E_2,N_2]=E_2
があれば、形式的に
[E_1E_2^{\dagger} , N_1+N_2] = 0
[E_1E_2^{\dagger} , N_1-N_2] = 2E_1E_2^{\dagger}
と計算できる。E_1E_2^{\dagger}は、Susskind-Glogower演算子を使って書いた位相差演算子に相当する。少し条件を弱めて、
[E_{12} , N_1+N_2]= 0 , [E_{12} , N_1-N_2] = 2E_{12}
としたものが、条件(2.5a)(2.5b)。この2条件を満たすユニタリー演算子E_{12}が存在するか否かを考えてみることができる。論文では、古典的なPoisson括弧による関係式の量子化として、条件(2.5a)(2.5b)を書いている。いずれにせよ、この2つの条件は、成立してほしいと考える理由がある。


理想的な位相差演算子が存在しないことの証明は、以下の通り。条件(2.5b)から、位相差演算子と、相対粒子数演算子は閉じた代数をなし、位相差演算子がユニタリーであることを要求すると、二次元Euclid代数のユニタリー表現が定まることになる。ユニタリー性から位相差演算子は0でないけど、その場合、二次元Euclid代数のユニタリー表現は、必ず、無限次元である。一方、条件(2.5a)から、この二次元Euclid代数の作用は、総粒子数演算子と可換で、二次元Euclid代数の作用は、総粒子数一定の空間で閉じる必要がある。総粒子数nの部分空間の次元は、n+1で有限だから、条件(2.5a)(2.5b)と位相差演算子のユニタリー性を同時に満たすことはできない

常識的に考えれば、一方の粒子数が0の時は、干渉させることはできないので、位相差は定義できない。実際に、条件(2.5a)(2.5b)を満たすように位相差演算子を決めようとすると、問題を起こすのは、どっちかの粒子数が0の場合なので、問題の根源は、単一モードの時と変わらないと思われる。また、Stokesパラメータには、位相差のcosとsinに比例するパラメータがあり、通常、atanを計算することで、位相差がわかるが、一方の強度が0の場合、この2つのパラメータは、どっちも0になってしまい、位相差は不定となる

可能な選択肢は3つある。
(1)ユニタリー性を諦める。この場合、条件を満たす演算子は、Susskind-Glogower演算子を使って書けるものに限ることが示せる
(2)条件(2.5a)を諦める。RNS位相演算子や、Shapiro-Wagner位相演算子というもの(※)が知られていて、二乗すれば、条件(2.5b)を満たすユニタリー演算子となる
(3)条件(2.5b)を諦める。この場合、可能な演算子は、論文の式(2.13)で定義されるものに限る。論文著者の名前を採って、Luis-Sanchez-Sotoの(位相差)演算子と呼ばれることがある


※)RNS位相演算子については、以下に日本語の解説がある(RNS位相演算子は、一方のモードを、真空状態に取ることで、もう一方の位相を定義している)
位相演算子とその応用 : 量子光学系におけるコヒーレンスと散逸
https://repository.kulib.kyoto-u.ac.jp/dspace/handle/2433/94961

Shapeiro-Wagnerの論文は、以下であるけど、Shapiro-Wagner位相演算子を実際に導入したのは、Hradilという人のようである
Phase and amplitude uncertainties in heterodyne detection
https://ieeexplore.ieee.org/document/1072470

Shapiro-Wagner位相演算子とRNS位相演算子がユニタリ同値だということは、以下で主張されている
Unitary equivalence between ideal and feasible phases
https://journals.aps.org/pra/abstract/10.1103/PhysRevA.50.2785


理想的な位相差演算子は存在せず、少なくとも、4つの位相差演算子の候補がある。多分、どれが正しい定義とかいうのはなくて、どの位相差演算子も("実部"と"虚部"に分解すればエルミートだから)測定できる可能性はある

Airy関数、奴は超幾何四天王の中でも最弱

何とはなしに目にした論文arXiv:1401.0025で、超双曲方程式から、Airyの微分方程式への次元簡約が与えられていた。Gauss超幾何関数について、類似の簡約は、Selected topics in integral geometryという本のChapter2の1.2節が、"John transform and Gauss hypergeometric function"というタイトルで、その中に与えられている。後者の本では、積分変換から、やや天下り的に与えられている。

他のGauss超幾何関数の眷属(Kummer,Hermite-Weber,Bessel)についても、同様の次元簡約が存在するけど、明示的に書かれてるのを見たことがないので、以下で計算した。

超双曲方程式から超幾何型関数への簡約
https://vertexoperator.github.io/2018/11/28/reduction_of_ultrahypebolic_equation.html

特に、難しい議論とかはなくて、面倒な算数をやるだけ。これらの次元簡約は、Gauss超幾何関数を、Grassmann多様体上のGelfand超幾何系として実現する時にも、現れているので新しいものじゃない。Gelfand超幾何系を定義する標準的なやり方は、Z \subset Mat(2,4)を、GL(2)の左作用と、GL(4)の3次元可換部分群Hで割るというもの。代わりに、(確認してないけど)、Mat(2,4)の部分集合上で定義されるGrassmann超幾何系の主要部分を、左からのGL(2)作用で簡約したら、超双曲方程式になるのだろう。で、残りのHの方で、超双曲方程式を簡約する、というのが、上に書いた話になる。GL(2)で割った後に出てくる多様体は、Grassmann多様体Gr(2,\mathbb{C}^4で、これは、4次元だから、これを1次元に簡約するには、4-1=3次元以上の群が必要になる。簡約に使われる群は、GL(4)の極大可換部分群で、全て3次元になっている。

Gelfand超幾何関数の文脈では、可換群Hの無限小作用が書かれてることは少ない気がするけど、同様の群は、MasonとWoodhouseの"Integrability, Self-duality, and Twistor Theory"という本では、Painleve groupsという名前で、無限小作用の形と共に与えられている(本のTable7.2と、その周辺)。Painleve groupsという名前は、SL(2,C)-ASDYM(反自己双対Yang-Mills)方程式を、同様に次元簡約した場合、Painleve方程式が出るので、そう名付けたようである。超幾何関数のことも考えると、いい名前とも思えないし、書籍の出版から20年以上経っても、特に普及した名称とはなってないと思う。

論文としては、

Self-duality and the Painleve transcendents
http://iopscience.iop.org/article/10.1088/0951-7715/6/4/004

があるけど、様々な人が、ばらばらに発見していた次元簡約を、MasonとWoodhouseが、まとめたということっぽい


超双曲方程式は、物理でも、数学でも、それほど注目されることがない。1938年に、Firtz Johnという人が、解を積分変換で書けるという論文を書いたらしく、それに因んで、John's equationと呼ばれることもあるらしい。

John's equation
https://en.wikipedia.org/wiki/John%27s_equation

これは、後に、twistor理論で発見されたPenrose変換と同種のもので、20世紀初頭には、WhittakerとBatemanが、3次元と4次元Laplace方程式に対して、類似の結果を与えていた(全然理解してないけど、3次元Laplace方程式の方は、mini-twistorの文脈で理解できるらしい)。

Selected topics in integral geometryでは、Fritz Johnが与えた積分変換から、超幾何積分を作っている。


超双曲方程式は、ナイーブにはEuclid空間上で定義されていて、一見すると、超幾何関数を連想するものは、何もないけど、その共形対称性は、Spin(3,3) \simeq SL(4,\mathbb{R})で与えられる。この共形対称性から、共形コンパクト化を考えると、(S^2 \times S^2)/\{\pm 1\}であるけど、これは、Grassmann多様体Gr(2,\mathbb{R}^4)と同型なので、Grassmann多様体とは浅くない因縁がある。複素化した無限小共形対称性は、\mathfrak{sl}(4,\mathbb{C})であるけど、これは、Gauss超幾何関数の隣接関係式を与える"対称性"となる。隣接関係式が、"対称性"に見えるという事実の発見者が、誰なのかよく分からないけど、Willard Miller, Jr.という人が、それらしいことを書いている(1970年代初め頃)

Lie Theory and the Lauricella Functions FD
https://aip.scitation.org/doi/abs/10.1063/1.1666152

Lie Theory and the Appell Functions $F_1$
https://epubs.siam.org/doi/abs/10.1137/0504055

Lie Theory and Generalizations of the Hypergeometric Functions
https://epubs.siam.org/doi/10.1137/0125026

Symmetries of Differential Equations. The Hypergeometric and Euler–Darboux Equations
https://epubs.siam.org/doi/10.1137/0504030

Millerは、dynamical symmetry algebraという言葉を使っていて、論文を読むと、(Gauss超幾何の場合)、形式的に、3つの変数を追加していたりする。当時は、その意味は、よく分からなかったのじゃないかと思うけど、現在から見ると、次元簡約で失われた3つの変数を復活させていると理解できる。この変数の意味は、Gelfand超幾何系から始めるよりも、超双曲方程式から始めたほうが、見やすい。


超双曲方程式の解は、Fritz Johnによって、積分変換の形で与えられた(X-ray transformと呼ばれることもある)。これは、massless Klein-Gordon方程式の解を、Penrose変換で書く話と、親戚みたいなものになっている。massless Klein-Gordon方程式の解が、SU(2,2)の極小表現を与えたのと同様の意味で、超双曲方程式の解は、SL(4,\mathbb{R})の"極小表現"を与える。詳細は、以下の論文などが良いと思う

The Penrose Transform in the Split Signature
https://arxiv.org/abs/0812.3692

論文では、split Penrose transformという名称が使われている。Penroseは、3つのタイプのPenrose変換の最後の一つを見つけたので、priorityの観点からは、Penrose変換と呼ぶのはどうかという気もするけど、twistor理論が出るまで、特に注目されずにいた結果なので、仕方ない。

そういうわけで、大雑把には、Gauss超幾何関数<->超双曲方程式<->SL(4,\mathbb{R})の"極小表現"という繋がりがある。一般化の方向性としては、
(1)q-変形を考える
(2)Appell-Lauricella超幾何関数<->???<->SL(n,\mathbb{R})の何らかの既約ユニタリ表現
などが思いつく。もうやってる人がいるかもしれないけど